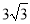题目内容
如图1,平面直角坐标系 中,点
中,点 ,OC=8,若抛物线
,OC=8,若抛物线 平移后经过C,D两点,得到图1中的抛物线W.
平移后经过C,D两点,得到图1中的抛物线W.
(1)求抛物线W的表达式及抛物线W与 轴另一个交点
轴另一个交点 的坐标;
的坐标;
(2)如图2,以OA,OC为边作矩形OABC,连结OB,若矩形OABC从O点出发沿射线OB方向匀速运动,速度为每秒1个单位得到矩形 ,求当点
,求当点 落在抛物线W上时矩形的运动时间;
落在抛物线W上时矩形的运动时间;
(3)在(2)的条件下,如图3,矩形从O点出发的同时,点P从 出发沿矩形的边
出发沿矩形的边 以每秒
以每秒 个单位的速度匀速运动,当点P到达
个单位的速度匀速运动,当点P到达 时,矩形和点P同时停止运动,设运动时间为
时,矩形和点P同时停止运动,设运动时间为 秒.
秒.
①请用含 的代数式表示点P的坐标;
的代数式表示点P的坐标;
②已知:点P在边 上运动时所经过的路径是一条线段,求点P在边
上运动时所经过的路径是一条线段,求点P在边 上运动多少秒时,点D到CP的距离最大.
上运动多少秒时,点D到CP的距离最大.


(1)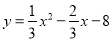 ,6,0);(2)
,6,0);(2)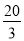 ;(3)①∴当
;(3)①∴当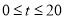 时,
时,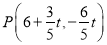 ,当
,当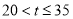 时,
时,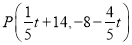 ;②
;②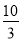 .
.
【解析】
试题分析:(1)先得到C的坐标,再把D、C的坐标代入平移后的解析式即可,令y=0,可以得到和x轴的另一交点的坐标;
(2)经过t秒后,点 的坐标为:
的坐标为: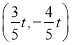 ,将
,将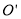 代入
代入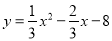 ,即可求出
,即可求出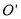 落在抛物线
落在抛物线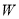 上的时间;
上的时间;
(3)① 设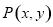 ,分两种情况讨论:(I)当
,分两种情况讨论:(I)当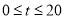 时,即点P在
时,即点P在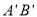 边上,(II)当
边上,(II)当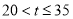 时,即点P在
时,即点P在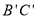 边上(不包含
边上(不包含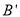 点),
点),
②当点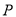 在
在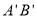 运动时,
运动时,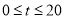 ,可以求出点P所经过的路径所在函数解析式,还可以求出直线
,可以求出点P所经过的路径所在函数解析式,还可以求出直线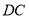 解析式为:
解析式为: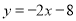 ,得到DC∥AP,从而有△DCP面积为定值.当CP取得最小值时,点D到CP的距离最大,即当CP⊥AP时,CP取得最小值.
,得到DC∥AP,从而有△DCP面积为定值.当CP取得最小值时,点D到CP的距离最大,即当CP⊥AP时,CP取得最小值.
试题解析:(1)依题意得: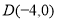 ,
,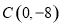 ,∴抛物线
,∴抛物线 的解析式为:
的解析式为: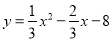 ,另一交点为(6,0);
,另一交点为(6,0);
(2)依题意:在运动过程中,经过t秒后,点 的坐标为:
的坐标为: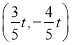 ,将
,将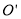 代入
代入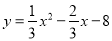 ,舍去负值得:
,舍去负值得: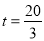 ,经过
,经过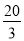 秒
秒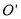 落在抛物线
落在抛物线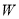 上;
上;
(3)① 设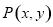 ,
,
(I)当 时,即点P在
时,即点P在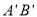 边上,
边上,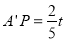 ,
, ,∴
,∴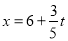 ,
,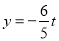 ;
;
(II)当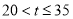 时,即点P在
时,即点P在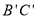 边上(不包含
边上(不包含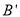 点),
点),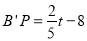 ,
,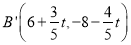 ,∴
,∴ ,
,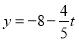 ,
,
综上所述:∴当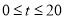 时,
时,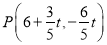 ,当
,当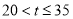 时,
时,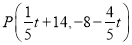 ,
,
②当点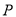 在
在 运动时,
运动时,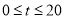 ,点P所经过的路径所在函数解析式为:
,点P所经过的路径所在函数解析式为: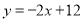 ,又∵直线
,又∵直线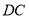 解析式为:
解析式为: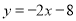 ,∴DC∥AP,∴△DCP面积为定值.∴CP取得最小值时,点D到CP的距离最大,如图,当CP⊥AP时,CP取得最小值,过点P作PM⊥y轴于点M,∴∠PMC=90°,∵
,∴DC∥AP,∴△DCP面积为定值.∴CP取得最小值时,点D到CP的距离最大,如图,当CP⊥AP时,CP取得最小值,过点P作PM⊥y轴于点M,∴∠PMC=90°,∵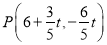 ,∴
,∴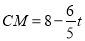 ,
,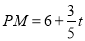 ,∵∠DCO+∠PCM=90°,∠CPM+∠PCM=90°,∴
,∵∠DCO+∠PCM=90°,∠CPM+∠PCM=90°,∴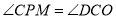 ,∴
,∴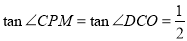 ,在Rt△PMC中,∠PMC=90°,∴
,在Rt△PMC中,∠PMC=90°,∴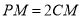 , ∴
, ∴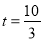 ,检验:
,检验: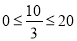 ,∴经过
,∴经过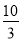 秒时,点D到CP的距离最大.
秒时,点D到CP的距离最大.

考点:二次函数综合题.

 的方程
的方程 .
.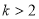 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根; 的图象与x轴交于A,B两点(A在B的左侧),与
的图象与x轴交于A,B两点(A在B的左侧),与 轴交于点C,且tan∠OAC=4,求该二次函数的解析式;
轴交于点C,且tan∠OAC=4,求该二次函数的解析式; 的图象于点N.若只有当
的图象于点N.若只有当 时,点M位于点N的下方,求一次函数
时,点M位于点N的下方,求一次函数 的解析式.
的解析式.
 ,另两条直线分别交
,另两条直线分别交 ,
, ,
, 于点
于点 及点
及点 ,且
,且 ,
, ,
, ,那么下列等式正确的是( )
,那么下列等式正确的是( )
 B.
B.
 D.
D.
 被⊙P
被⊙P ,则点P的坐标为 .
,则点P的坐标为 . 
 的顶点坐标为( )
的顶点坐标为( )  B.
B. C.
C. D.
D. 

 .
.
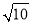 ,AD=2,求线段PC的长.
,AD=2,求线段PC的长.
 B.
B.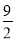 C.
C.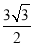 D.
D.