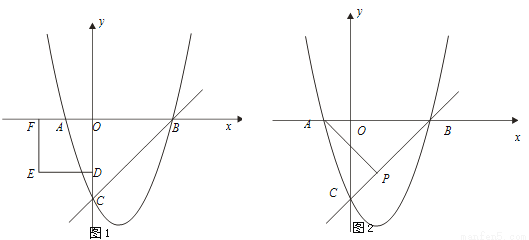
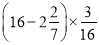题目内容
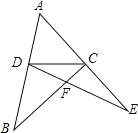
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
A.114° B.123° C.132° D.147°
B. 【解析】 试题分析:∵BD=CD=CE,等腰三角形的性质得出∠B=∠DCB,∠E=∠CDE, ∵∠ADC+∠ACD=114°,∴∠BDC+∠ECD=360°﹣114°=246°, ∴∠B+∠DCB+∠E+∠CDE=360°﹣246°=114°, ∴∠DCB+∠CDE=57°, ∴∠DFC=180°﹣57°=123°, 故选B.
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目


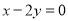 B.
B. 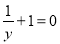 C.
C. 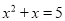 D.
D. 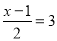
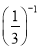 +16÷(﹣2)3+(2005﹣π)0﹣
+16÷(﹣2)3+(2005﹣π)0﹣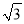 tan30°
tan30°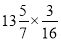 时,下列变形最简便的是( )
时,下列变形最简便的是( )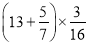 B.
B. 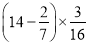 C.
C.  D.
D.