题目内容
 如图,在?ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )
如图,在?ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于( )| A、2 | B、3 | C、4 | D、5 |
考点:三角形中位线定理,平行四边形的性质
专题:
分析:由四边形ABCD是平行四边形,根据平行四边形的对边相等,可得BC=AD=8,又由点E、F分别是BD、CD的中点,利用三角形中位线的性质,即可求得答案.
解答:解:∵四边形ABCD是平行四边形,
∴BC=AD=8,
∵点E、F分别是BD、CD的中点,
∴EF=
BC=
×8=4.
故选C.
∴BC=AD=8,
∵点E、F分别是BD、CD的中点,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:此题考查了平行四边形的性质与三角形中位线的性质.此题比较简单,注意掌握数形结合思想的应用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 如图,直线l1∥l2,若∠1=135°,∠2=65°,则∠3的度数是( )
如图,直线l1∥l2,若∠1=135°,∠2=65°,则∠3的度数是( )| A、70° | B、80° |
| C、65° | D、60° |
下列各式中,是3a2b的同类项的是( )
| A、2x2y |
| B、-2ab2 |
| C、a2b |
| D、3ab |
下列说法正确的是( )
A、0.
| ||||
B、
| ||||
C、
| ||||
| D、0.13579…(小数部分由连续的奇数组成)是无理数 |
等腰三角形的腰为3,底为2,下列说法不正确的是( )
| A、底边上的高为有理数 |
| B、它的周长为有理数 |
| C、它的面积不是有理数 |
| D、腰上的高不是有理数 |
 如图,△ABC中AB=2,BC=3,∠B=60°,△ABC的周长是
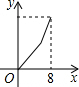
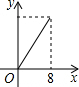
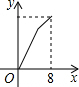
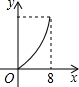
如图,△ABC中AB=2,BC=3,∠B=60°,△ABC的周长是 如图,在长方形ABCD中,CD=5,BC=3,点P从起点D出发沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y.在下列图象中,能正确反映y与x的函数关系的是( )
如图,在长方形ABCD中,CD=5,BC=3,点P从起点D出发沿DC、CB向终点B匀速运动.设点P所走过的路程为x,点P所经过的线段与线段AD、AP所围成图形的面积为y.在下列图象中,能正确反映y与x的函数关系的是( )