题目内容
如图，某拦河坝截面的原设计方案为：坝高为6m，坡角∠ABC=60°．为了提高拦河坝的安全性，现将坡角改为45°，由此，点A需向右平移至点D，求AD的长．（参考数据：
≈1.732）．
解：分别过A、D两点作AE⊥BC于E，DF⊥BC于F，
在Rt△BDF中，
∵∠DBF=45°，
∴DF=BF=AE=6，
在Rt△ABE中，
∵tan∠DBF=tan60°=
，
∴BE=
，
∴AD=EF=BF-BE=6-≈2.54（m）．
分析：分别过A、D两点作AE⊥BC于E，DF⊥BC于F，根据坡角，在Rt△ABE和Rt△BDF中，分别求出BF和BE的长度，然后即可求解．
点评：本题考查了学生对坡度坡角的掌握及三角函数的运用能力，解题的关键构造直角三角形，利用解直角三角形的知识求出BE，BF的长度．
在Rt△BDF中，
∵∠DBF=45°，
∴DF=BF=AE=6，
在Rt△ABE中，
∵tan∠DBF=tan60°=
，∴BE=
，∴AD=EF=BF-BE=6-
≈2.54（m）．分析：分别过A、D两点作AE⊥BC于E，DF⊥BC于F，根据坡角，在Rt△ABE和Rt△BDF中，分别求出BF和BE的长度，然后即可求解．
点评：本题考查了学生对坡度坡角的掌握及三角函数的运用能力，解题的关键构造直角三角形，利用解直角三角形的知识求出BE，BF的长度．
练习册系列答案
相关题目
如图，⊙O的直径AB与弦CD相交于点M，AE⊥CD于E，BF⊥CD于F．若CM=4，MD=3，BF：AE=1：3，则⊙O的半径是________．
如图，有相邻的两块长方形土地，大小如图所示（a＞100，单位m），出售土地的价格有如下两种不同方式：
万元/m2（1）填表：
| α | 0.001 | 1 | 1000 | 1000000 |
 | ______ | ______ | ______ | ______ |
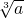（3）根据你发现的规律填空：
①已知
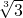=1.442，则
=______，②已知
=0.07696，则
=______；（4）用铁皮制作一个封闭的正方体，它的体积为0.456立方米，问需要多大面积的铁皮？（结果精确到0.1平方米）
在矩形ABCD中，AB=a，AD=2b（a＞2b＞0），E是AD的中点，BF⊥EC，垂足为F，求BF的长（用含有a、b的代数式表示）．
得________．