题目内容
17．$\sqrt{（3-2x）^{2}}$=2x-3，x的取值范围是x≥$\frac{3}{2}$．分析 根据公式$\sqrt{{a}^{2}}$=|a|，可得出x的取值范围．
解答 解：∵$\sqrt{（3-2x）^{2}}$=2x-3，
∴3-2x≤0，
解得x≥$\frac{3}{2}$，
∴x的取值范围是x≥$\frac{3}{2}$，
故答案为x≥$\frac{3}{2}$．
点评 本题考查了二次根式的性质和化简，熟记公式$\sqrt{{a}^{2}}$=|a|=$\left\{\begin{array}{l}{a（a≥0）}\\{-a（a＜0）}\end{array}\right.$是解题的关键．
练习册系列答案
53随堂测系列答案
相关题目
10．四张背面完全一样圆形纸片，正面图案如下，将这四张纸片背面朝上摞在一起洗，匀后从中随机抽取2张，其中有中心对称图形的概率是（ ）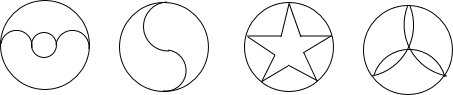
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
如图所示，一个不等式组的解集表示在数轴上，这个不等式组可能是$\left\{\begin{array}{l}{x≤3}\\{x＞-1}\end{array}\right.$．
2．
如图把两个不等式的解集表示在数轴上，则这两个不等式组成的不等式组可能是（ ）
如图把两个不等式的解集表示在数轴上，则这两个不等式组成的不等式组可能是（ ）| A． | $\left\{\begin{array}{l}{x＜4}\\{x≥-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x＞4}\\{x≤1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x＞4}\\{x＞-1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x≤4}\\{x＞-1}\end{array}\right.$ |
9．下列二次根式中属于最简二次根式的是（ ）
| A． | $\sqrt{a+1}$ | B． | $\sqrt{\frac{a}{b}}$ | C． | $\sqrt{{a}^{2}b}$ | D． | $\sqrt{9a}$ |
6．
如图，m∥n，∠1+∠2=80°，则∠3+∠4的度数为（ ）
如图，m∥n，∠1+∠2=80°，则∠3+∠4的度数为（ ）| A． | 60° | B． | 80° | C． | 100° | D． | 120° |