题目内容
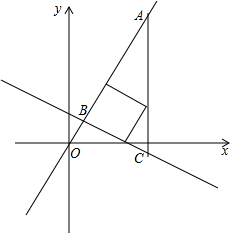 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-| 1 |
| 2 |
| 5 |
| 2 |
(1)求∠OBC的度数;
(2)若正方形的四个顶点恰好在射线AB、射线CB及线段AC上,请直接写出射线AB上的正方形顶点的坐标.(不需要写出计算过程).
考点:一次函数综合题
专题:
分析:(1)首先求得C的坐标,即可求得A的坐标,然后利用待定系数法求得AB的解析式,即可作出判断;
(2)首先求得△ABC的三边长,然后利用相似三角形的性质求得正方形的边长,则正方形上射线AB上的点F到O的距离,OF即可求得,然后作FG⊥x轴于点G,根据三角形相似即可求得F的坐标.
(2)首先求得△ABC的三边长,然后利用相似三角形的性质求得正方形的边长,则正方形上射线AB上的点F到O的距离,OF即可求得,然后作FG⊥x轴于点G,根据三角形相似即可求得F的坐标.
解答:解:(1)在y=-
x+
,中令x=7,则y=-
×7+
=-1,
∵AC=15,
∴A的纵坐标是14,则A的坐标是(7,14),
把(7,14)代入y=kx得:7k=14,
解得:k=2,
∵2×(-
)=-1,
∴直线AB和BC垂直,
∴∠OBC=90°;
(2)根据题意得:
,
解得:
,
则B的坐标是(1,2),
0B=
=
.
AB=
=6
,BC=
=3
,
设正方形BDEF的边长是x,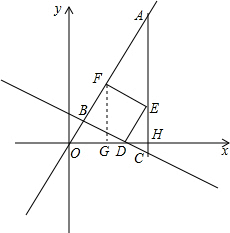
则△AFE∽△ABC,
则
=
,即
=
,
解得:x=2
,
则OF=
+2
=3
,
OA=
=7
,
作FG⊥x轴于点G.
∵FG∥AH,
∴△FOG∽△AOH,
∴
=
=
=
,
∴FG=
AH=
×14=6,则F的纵坐标是7,
把y=6代入y=2x得:x=3.
则F的坐标是(3,6).
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵AC=15,
∴A的纵坐标是14,则A的坐标是(7,14),
把(7,14)代入y=kx得:7k=14,
解得:k=2,
∵2×(-
| 1 |
| 2 |
∴直线AB和BC垂直,
∴∠OBC=90°;
(2)根据题意得:
|
解得:
|
则B的坐标是(1,2),
0B=
| 12+22 |
| 5 |
AB=
| (7-1)2+(14-2)2 |
| 5 |
| (7-1)2+(2+1)2 |
| 5 |
设正方形BDEF的边长是x,

则△AFE∽△ABC,
则
| EF |
| BC |
| AF |
| AB |
| x | ||
3
|
6
| ||
6
|
解得:x=2
| 5 |
则OF=
| 5 |
| 5 |
| 5 |
OA=
| 72+142 |
| 5 |
作FG⊥x轴于点G.
∵FG∥AH,
∴△FOG∽△AOH,
∴
| FG |
| AH |
| OF |
| OA |
3
| ||
7
|
| 3 |
| 7 |
∴FG=
| 3 |
| 7 |
| 3 |
| 7 |
把y=6代入y=2x得:x=3.
则F的坐标是(3,6).
点评:本题考查了待定系数法求函数的解析式,直线互相垂直的条件,以及相似三角形的判定与性质,求得正方形BDEF的边长是关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
下列说法中,正确的是( )
A、开不尽的平方根和立方根,如
| |||||
B、不可约分数,如
| |||||
| C、无理数是指开不尽的方根(平方根,立方根等) | |||||
| D、数轴上的每一个点都有一个有理数和它对应 |
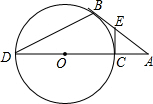 如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.
如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.
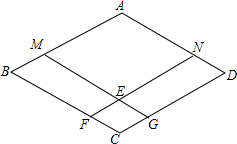 如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.
如图,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E,求证:四边形AMEN、EFCG都是菱形.