题目内容
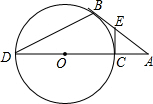 如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.
如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.(1)求∠D的度数;
(2)过C点作⊙O的切线交AB于E,若CE=2,求⊙O的半径.
考点:切线的性质,等腰三角形的性质,含30度角的直角三角形
专题:
分析:(1)如图,作辅助线;求出∠BOA=60°;证明∠D=∠DBO即可解决问题.
(2)求出AE、AB的长,借助直角三角形的边角关系即可解决问题.
(2)求出AE、AB的长,借助直角三角形的边角关系即可解决问题.
解答: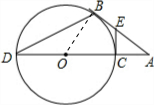 解:(1)如图,连接OB,
解:(1)如图,连接OB,
∵AB是⊙O的切线‘
∴∠ABO=90°;
∵∠A=30°,
∴∠BOA=60°,
∴∠D+∠DBO=60°;
∵OD=OB,
∴∠D=∠DBO=30°.
(2)∵CE是⊙O的切线,
∴∠OCE=90°
∴∠ECA=90°,
∵∠A=30°,
∴EA=2CE=4;
∵AB、CE是⊙O的切线,
∴BE=CE=2,
∴AB=2+4=6;
∵tan30°=
,
∴OB=2
,
即⊙O的半径为2
.
 解:(1)如图,连接OB,
解:(1)如图,连接OB,∵AB是⊙O的切线‘
∴∠ABO=90°;
∵∠A=30°,
∴∠BOA=60°,
∴∠D+∠DBO=60°;
∵OD=OB,
∴∠D=∠DBO=30°.
(2)∵CE是⊙O的切线,
∴∠OCE=90°
∴∠ECA=90°,
∵∠A=30°,
∴EA=2CE=4;
∵AB、CE是⊙O的切线,
∴BE=CE=2,
∴AB=2+4=6;
∵tan30°=
| OB |
| AB |
∴OB=2
| 3 |
即⊙O的半径为2
| 3 |
点评:该题主要考查了圆的切线及其应用问题;解题的关键是作辅助线,构造直角三角形,灵活运用切线的性质、直角三角形的边角关系等几何知识来分析、解答.

练习册系列答案
相关题目
下列说法正确的是( )
| A、在墙上固定一根木条,至少需要2颗钉子 |
| B、射线OA和射线AO是同一条射线 |
| C、延长直线AB |
| D、线段AB和线段BA不是同一条线段 |
下列各组单项式中,不是同类项的是( )
A、12y与
| ||||
| B、6mb与-bm | ||||
| C、23与32 | ||||
D、
|
 已知∠BAC=90°,AB=AC,AD⊥BC,BE=AF,DE=10.求:
已知∠BAC=90°,AB=AC,AD⊥BC,BE=AF,DE=10.求: 如图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是
如图,若把△ABC绕A点顺时针旋转一定角度,就得到△ADE,请写出图中所有的对应边是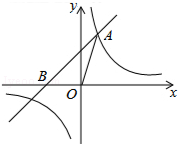 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=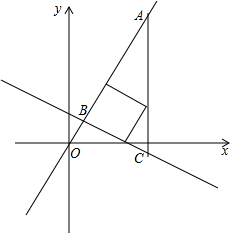 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-