Question

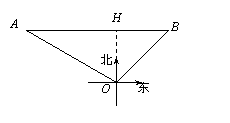
在海上某固定观测点O处的北偏西60°方向，且距离O处40海里的A处，有一艘货轮正沿着正东方向匀速航行，2小时后，此货轮到达O处的北偏东45°方向的B处．在该货轮从A处到B处的航行过程中．

   （1）求货轮离观测点O处的最短距离；

   （2）求货轮的航速．

   

Answer 1

解：（1）如图，作OH⊥AB，垂足为H．

在Rt△AOH中，∵cos∠AOH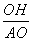＝．∴OH＝cos60°·AO＝20．

即货轮离观测点O处的最短距离为20海里．                                                   4分

（2）在Rt△AOH中，∵sin∠AOH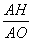＝，∴AH＝sin60°·AO＝20，

在Rt△BOH中，∵∠B＝∠HOB＝45°，∴HB＝HO＝20．

∴AB＝20＋20，

∴货轮的航速为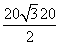＝10＋10（海里/小时）．                                     8分