题目内容
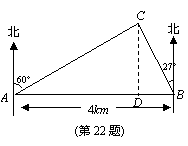
如图，在一笔直的海岸线上有A、B两个观测点，B在A的正东方向，AB＝4km．
从A测得灯塔C在北偏东60°的方向，从B测得灯塔C在北偏西27°的方向，求灯
塔C与观测点A的距离（精确到0.1km）．
(参考数据:sin27°≈0.45，cos27°≈0.90，tan27°≈0.50，
≈1.73)
 |
解：过点C作CD⊥AB，
则∠BCD＝27°，∠ACD＝60°， …………1分
在Rt△BDC中，由tan ∠BCD＝
，
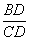∴BD＝CD tan27°＝0．5CD； …………3分
在Rt△ADC中，由tan ∠ACD＝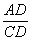
∴AD＝CD tan60°＝CD； …………4分
∵AD＋BD＝CD＋0.5CD＝4，
∴CD＝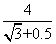
． …………5分
在Rt△ADC中，∵∠ACD＝60°，∴∠CAD＝30°，
∴AC＝2CD＝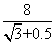
≈3.6．
∴灯塔C与观测点A的距离为3.6 km．…………7分
如图1，对于平面上小于等于
的
，我们给出如下定义：若点P在
的内部或边上，作
于点E，
于点
，则将
称为点
P与的“点角距”，记作d(∠MON，P)．如图2，在平面直角坐标系xoy中，
x、y正半轴所组成的角为∠xOy．
 |
（1）已知点A（5，0）、点B（3，2），则d(∠xOy，A) ＝ ，d(∠xOy，B) ＝ ．
（2）若点P为∠xOy内部或边上的动点，且满足d(∠xOy，P)＝5，画出点P运动所
形成的图形．
（3）如图3与图4，在平面直角坐标系xoy中，射线OT的函数关系式为y＝
x（x≥0）．
①在图3中，点C的坐标为（4，1），试求d(∠xOT，C)的值；
②在图4中，抛物线y＝－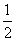
x 2＋2x＋
经过A（5，0）与点D(3，4)两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d(∠xOT，Q)取最大值时点Q 的坐标．
有意义的x的取值范围是 ．
任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是（ ）
（B）
（C）
（D）
