题目内容
6.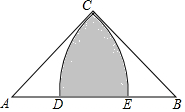 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作$\widehat{CE}$交AB于点E,以点B为圆心,BC的长为半径作$\widehat{CD}$交AB于点D,则阴影部分的面积为π-2.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作$\widehat{CE}$交AB于点E,以点B为圆心,BC的长为半径作$\widehat{CD}$交AB于点D,则阴影部分的面积为π-2.
分析 空白处的面积等于△ABC的面积减去扇形BCD的面积的2倍,阴影部分的面积等于△ABC的面积减去空白处的面积即可得出答案.
解答 解:∵∠ACB=90°,AC=BC=2,
∴S△ABC=$\frac{1}{2}$×2×2=2,
S扇形BCD=$\frac{45π•{2}^{2}}{360}$=$\frac{1}{2}$π,
S空白=2×(2-$\frac{1}{2}$π)=4-π,
S阴影=S△ABC-S空白=2-4+π=π-2,
故答案为π-2.
点评 本题考查了扇形的面积公式,正确理解公式是关键.

练习册系列答案
相关题目
16.π是$\frac{1}{π}$的( )
| A. | 绝对值 | B. | 倒数 | C. | 相反数 | D. | 平方根 |
18.下列计算正确的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | x8÷x2=x4 | C. | (2a)3=6a3 | D. | 3a3•2a2=6a6 |
16.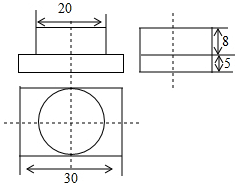 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
 如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )
如图是某几何体的三视图,根据图中的数据,求得该几何体的体积为( )| A. | 800π+1200 | B. | 160π+1700 | C. | 3200π+1200 | D. | 800π+3000 |
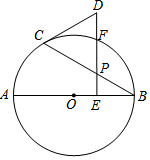 如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.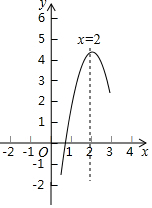 如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)
如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)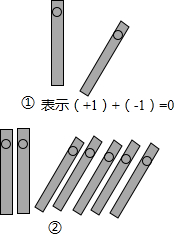 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.
中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.