题目内容
12. 在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、BC上,且DE=DF,则∠BED与∠BFD的关系是互补.
在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、BC上,且DE=DF,则∠BED与∠BFD的关系是互补.
分析 作DG⊥AB于G,DH⊥BC于H,根据角平分线的性质得到DH=DG,证明Rt△DEG≌Rt△DFH,得到∠DEG=∠DFH,根据互为邻补角的性质得到答案.
解答 解: 作DG⊥AB于G,DH⊥BC于H,
作DG⊥AB于G,DH⊥BC于H,
∵D是∠ABC平分线上一点,DG⊥AB,DH⊥BC,
∴DH=DG,
在Rt△DEG和Rt△DFH中,
$\left\{\begin{array}{l}{DG=DH}\\{DE=DF}\end{array}\right.$,
∴Rt△DEG≌Rt△DFH,
∴∠DEG=∠DFH,又∠DEG+∠BED=180°,
∴∠BFD+∠BED=180°,
则∠BED与∠BFD的关系是互补,
故答案为:互补.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
2.早晨气温是-7℃,中午温度上升了11℃,半夜又下降了9℃,则半夜的气温是( )
| A. | 0℃ | B. | 2℃ | C. | -5℃ | D. | 9℃ |
 二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.
二次函数y=ax2+bx+c的图象如图所示,则b>0,b2-4ac>0,a-b+c<0.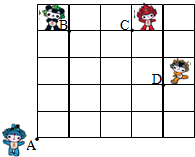 如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中,