题目内容
6．计算：1+x+x（1+x）+x（1+x）2+x（1+x）3+…+x（1+x）2011=（1+x）2012．分析 直接利用提取公因式法分解因式进而得出答案．
解答 解：1+x+x（1+x）+x（1+x）2+x（1+x）3+…+x（1+x）2011
=（1+x）[1+x+x（1+x）+x（1+x）2+x（1+x）3+…+x（1+x）2010]
=（1+x）（1+x）[1+x+x（1+x）+x（1+x）2+x（1+x）3+…+x（1+x）2009]
=（1+x）2012．
故答案为：（1+x）2012．
点评 此题主要考查了提取公因式法分解因式，正确找出公因式发现规律是解题关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
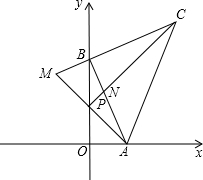如图，在平面直角坐标系中，已知两点A（m，0），B（0，n）（n＞m＞0），点C在第一象限，AB⊥BC，BC=BA，点P在线段OB上，OP=OA，AP的延长线与CB的延长线交于点M，AB与CP交于点N．
如图，将△ABC绕点B逆时针旋转90°后得到△A′BC′，则点A的对应点A′的坐标为（2，-3）．