题目内容
10. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O点,BC=AD,AO=5,则BO=5.
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O点,BC=AD,AO=5,则BO=5.
分析 根据全等三角形的判断和性质即可得到结论.
解答 解:∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°,
在△ADO与△BCO中,$\left\{\begin{array}{l}{∠D=∠C}\\{∠AOD=∠BOC}\\{AD=BC}\end{array}\right.$,
∴△ADO≌△BCO,
∴BO=AO=5.
故答案为:5.
点评 本题考查了全等三角形的判定与性质,解答本题的关键是熟练全等三角形的判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若(x+2)有平方根,则x的取值范围是( )
| A. | x<-2 | B. | x≤-2 | C. | x>2 | D. | x≥-2 |
5.已知点M(a,2),点N(3,b)关于y轴对称,则(a+b)2016=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
15.已知⊙O的半径为4,点P到点O的距离为3,则点P与⊙O的位置关系是( )
| A. | 在圆内 | B. | 在圆上 | C. | 在圆外 | D. | 不确定 |
19.某儿童服装店老板以每件50元的价格购进30件连衣裙,针对不同的顾客,30件连衣裙的售价不完全相同,若以每件70元为标准,将超过的钱数记为正,不足的钱数记为负,则记录结果如下表所示:
(1)该服装店在售完这30件连衣裙后,赚了多少钱?
(2)平均每件连衣裙赚了多少钱?
| 售出件数(件) | 7 | 6 | 3 | 5 | 4 | 5 |
| 售价(元) | -6 | -4 | 0 | +8 | +4 | +5 |
(2)平均每件连衣裙赚了多少钱?
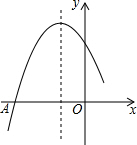 如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.
如图,二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1.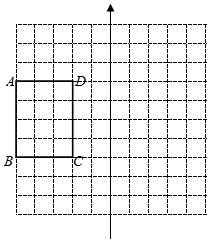 如图,已知长方形ABCD在平面直角坐标系(x轴和原点O均未画出)中,网格图中每个小正方形的边长都是1个单位长度,已知长方形ABCD在平面直角坐标系中关于x轴对称.
如图,已知长方形ABCD在平面直角坐标系(x轴和原点O均未画出)中,网格图中每个小正方形的边长都是1个单位长度,已知长方形ABCD在平面直角坐标系中关于x轴对称.