题目内容
13.(1)4x2-2xy+$\frac{1}{4}{y}^{2}$.(2)x(x-y)-y(y-x).
(3)1-m2-n2+2mn.
分析 (1)直接利用完全平方公式分解因式得出答案即可;
(2)直接提取公因式(x-y),进而求出答案即可;
(3)将后3项分组,进而利用完全平方公式以及平方差公式分解因式求出答案即可.
解答 解:(1)4x2-2xy+$\frac{1}{4}{y}^{2}$=(2x-$\frac{1}{2}$y)2;
(2)x(x-y)-y(y-x)
=x(x-y)+y(x-y)
=(x-y)(x+y);
(3)1-m2-n2+2mn
=1-(m2+n2-2mn)
=1-(m-n)2
=(1-m+n)(1+m-n).
点评 此题主要考查了公式法分解因式以及分组分解法分解因式,正确分组分解因式是解题关键.

练习册系列答案
相关题目
3.一次函数y=kx+b(k>0,b>0)的图象经过( )
| A. | 一、二、三象限 | B. | 一、二、四象限 | C. | 一、三、四象限 | D. | 二、三、四象限 |
8.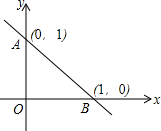 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
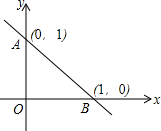 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
18. 下面的四幅图案可以通过平移图示得到的是( )
下面的四幅图案可以通过平移图示得到的是( )
 下面的四幅图案可以通过平移图示得到的是( )
下面的四幅图案可以通过平移图示得到的是( )| A. |  | B. |  | C. |  | D. |  |
5.筷子中有同样大小的红球1个、绿球2个,随机提出1个小球记下颜色后放回,再随机摸出1个,则两次摸到的球都是绿球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{9}$ |