题目内容
已知两个相似三角形的周边长比为2:3,且其中较大三角形的面积是36,那么其中较小三角形的面积是 .
考点:相似三角形的性质
专题:
分析:根据相似三角形的性质对应边成比例,面积比等于相似比的平方求解即可.
解答:解:两个相似三角形周长的比为2:3,
则相似比是2:3,
因而面积的比是4:9,
设小三角形的面积是4a,
则大三角形的面积是9a,
则9a=36,
解得a=4,
因而较小的三角形的面积是16.
故答案为:16.
则相似比是2:3,
因而面积的比是4:9,
设小三角形的面积是4a,
则大三角形的面积是9a,
则9a=36,
解得a=4,
因而较小的三角形的面积是16.
故答案为:16.
点评:本题考查对相似三角形性质的理解:(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
下列各图中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列结论:
Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列结论:①PE为⊙O的切线;②G为AC的中点;③OG∥BE;④∠A=∠P
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列图形既是轴对称图形又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于
如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于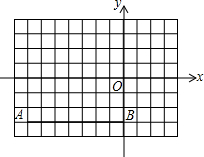 如图A(-7,-3)、B(0,-3),将线段AB先向上平移6个单位再向右平移3个单位得到线段A1B1,再将线段A1B1绕原点O顺时针旋转90°得到线段A2B2.
如图A(-7,-3)、B(0,-3),将线段AB先向上平移6个单位再向右平移3个单位得到线段A1B1,再将线段A1B1绕原点O顺时针旋转90°得到线段A2B2. 如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.
如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.