题目内容
 如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.
如图,⊙O中延长半径CO交弦AB于点P,∠OAB=30°,设∠OCB=α,∠COA=β.(1)当α=40°时,β=
(2)用含α的代数式表示β,则β=
(3)当α=30°时,求证:OC=2OP.
考点:圆周角定理,含30度角的直角三角形,多边形内角与外角
专题:
分析:(1)首先连接OB,可求得∠OBC与∠OBA的度数,继而求得∠BOC与∠AOB的度数,则可求得β的值;
(2)同理(1),可用含α的代数式表示β;
(3)由(2)可求得β的度数,即可得△AOP是直角三角形,继而可证得OC=2OP.
(2)同理(1),可用含α的代数式表示β;
(3)由(2)可求得β的度数,即可得△AOP是直角三角形,继而可证得OC=2OP.
解答: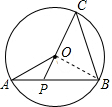 解:(1)连接OB,
解:(1)连接OB,
∵OB=OC=OA,∠OAB=30°,∠OCB=α=40°,
∴∠OBC=∠OCB=α=40°,∠A=∠OBA=30°,
∴∠BOC=180°-∠OBC-∠OCB=100°,∠AOB=180°-∠OAB-∠OBA=120°,
∴β=∠COA=360°-∠BOC-∠AOB=140°;
故答案为:140゜;
(2)连接OB,
∵OB=OC=OA,∠OAB=30°,∠OCB=α,
∴∠OBC=∠OCB=α,∠A=∠OBA=30°,
∴∠BOC=180°-∠OBC-∠OCB=180°-2α,∠AOB=180°-∠OAB-∠OBA=120°,
∴β=∠COA=360°-∠BOC-∠AOB=2α+60°;
故答案为:2α+60゜
(3)当α=30°时,β=2α+60゜=120゜,
∴∠OPA=120゜-30゜=90゜,
∵∠A=30゜,
∴OA=2OP,
∵OA=OC,
∴OC=2OP.
 解:(1)连接OB,
解:(1)连接OB,∵OB=OC=OA,∠OAB=30°,∠OCB=α=40°,
∴∠OBC=∠OCB=α=40°,∠A=∠OBA=30°,
∴∠BOC=180°-∠OBC-∠OCB=100°,∠AOB=180°-∠OAB-∠OBA=120°,
∴β=∠COA=360°-∠BOC-∠AOB=140°;
故答案为:140゜;
(2)连接OB,
∵OB=OC=OA,∠OAB=30°,∠OCB=α,
∴∠OBC=∠OCB=α,∠A=∠OBA=30°,
∴∠BOC=180°-∠OBC-∠OCB=180°-2α,∠AOB=180°-∠OAB-∠OBA=120°,
∴β=∠COA=360°-∠BOC-∠AOB=2α+60°;
故答案为:2α+60゜
(3)当α=30°时,β=2α+60゜=120゜,
∴∠OPA=120゜-30゜=90゜,
∵∠A=30゜,
∴OA=2OP,
∵OA=OC,
∴OC=2OP.
点评:此题考查了圆周角定理、等腰三角形的性质以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
二次项系数为1的一元二次方程的两根分别为
,
,那么这个方程为( )
-1+
| ||
| 2 |
-1-
| ||
| 2 |
| A、x2-x+1=0 |
| B、x2-x-1=0 |
| C、x2+x-1=0 |
| D、x2+x+1=0 |
 抛物线y=ax2+bx+c(a≠0)如图所示,下列4个结论正确的是( )
抛物线y=ax2+bx+c(a≠0)如图所示,下列4个结论正确的是( )| A、abc<0 |
| B、4a-2b+c>0 |
| C、2a+b>0 |
| D、4a+2b+c<0 |
 在Rt△ACD中,∠C=90°,∠ABD=135°,∠A=30°,BD=6,求AD的长度.
在Rt△ACD中,∠C=90°,∠ABD=135°,∠A=30°,BD=6,求AD的长度.