题目内容
某校九年级男生进行引体向上训练,体育老师随机选择了部分男生,根据训练前成绩编组:0~4个的编为第一组,5~8个的编为第二组,9~12个的编为第三组,在训练后制作了如下两幅统计图,请回答下列问题:
(1)下列说法正确的是 (填写所有正确的序号).
①训练后,第一组引体向上平均成绩的增长率最大;
②训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数一定在第二组.
(2)估计该校九年级全体男生训练后的平均成绩是多少?

(1)下列说法正确的是
①训练后,第一组引体向上平均成绩的增长率最大;
②训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数一定在第二组.
(2)估计该校九年级全体男生训练后的平均成绩是多少?

考点:条形统计图,用样本估计总体,扇形统计图,中位数,众数
专题:计算题
分析:(1)①求出训练后,各小组引体向上平均成绩的增长率,比较大小即可;
②根据扇形统计图得到第二组男生占60%,利用中位数的定义得到:训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数不一定在第二组;
(2)根据题意列出算式,计算即可得到结果.
②根据扇形统计图得到第二组男生占60%,利用中位数的定义得到:训练前,所选男生引体向上成绩的中位数一定在第二组;
③训练前,所选男生引体向上成绩的众数不一定在第二组;
(2)根据题意列出算式,计算即可得到结果.
解答:解:(1)根据题意得:①求出训练后,第一小组平均成绩的增长率为
=
;第二小组平均成绩的增长率为
=
;第三小组平均成绩的增长率为
=
,
则第一小组引体向上平均成绩的增长率最大,本选项正确;
②根据扇形统计图得到第二组男生占60%,利用中位数的定义得到:训练前,所选男生引体向上成绩的中位数一定在第二组,本选项正确;
③训练前,所选男生引体向上成绩的众数不一定在第二组,本选项错误;
(2)根据题意得:5×30%+8×60%+10×10%=7.3(个).
答:估计该校九年级全体男生训练后的平均成绩是7.3个.
故答案为:①②.
| 5-2 |
| 2 |
| 3 |
| 2 |
| 8-6 |
| 6 |
| 1 |
| 3 |
| 10-9 |
| 9 |
| 1 |
| 9 |
则第一小组引体向上平均成绩的增长率最大,本选项正确;
②根据扇形统计图得到第二组男生占60%,利用中位数的定义得到:训练前,所选男生引体向上成绩的中位数一定在第二组,本选项正确;
③训练前,所选男生引体向上成绩的众数不一定在第二组,本选项错误;
(2)根据题意得:5×30%+8×60%+10×10%=7.3(个).
答:估计该校九年级全体男生训练后的平均成绩是7.3个.
故答案为:①②.
点评:此题考查了条形统计图,扇形统计图,中位数,众数,以及用样本估计总体,弄清题意是解本题的关键.

练习册系列答案
相关题目
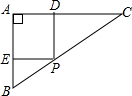 如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )
如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )A、4-
| ||||
B、
| ||||
C、
| ||||
D、
|
 下列图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )
下列图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )| A、36 | B、55 | C、70 | D、91 |
不等式组
的解集是( )
|
| A、x>2 | B、x≤3 |
| C、2<x≤3 | D、2≤x<3 |
 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则AB的长为( )| A、4 | B、6 | C、8 | D、10 |
 如图,边长为1的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕着点O逆时针旋转90°.
如图,边长为1的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕着点O逆时针旋转90°.