题目内容
如图,AB=DC,∠ A=∠D,点M和点N分别是BC、AD的中点.求证:∠ABC=∠DCB.
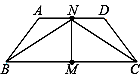 |
证明:点M和点N分别是BC、AD的中点,
∴AN=DN,BM=CM.
在△ABN和△DCN中
 ,
,
∴△ABN≌△DCN(SAS),
∴BN=CN,∠ABN=∠DCN.
在△BMN和△CMN中
 ,
,
∴△BMN≌△CMN,
∴∠MBN=∠MCN,
∴∠ABN+∠MBN=∠DCN+∠MCN,
即∠ABC=∠DCB.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
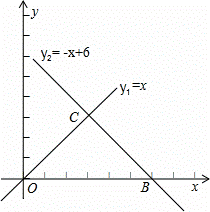
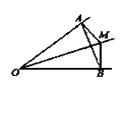
 的每个顶点处各需剪掉一个四边形,则
的每个顶点处各需剪掉一个四边形,则 MDN的度数为 .
MDN的度数为 .

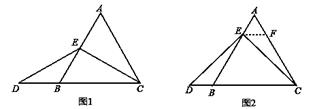 如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
如下:如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
 :(1)DE=DF; (2)AE=AF .
:(1)DE=DF; (2)AE=AF .
 有意义,那么x的取值范围是 ( )
有意义,那么x的取值范围是 ( ) D.x > −
D.x > −