题目内容
如图,直线OC,BC的函数关系式分别y1=x和y2=-x+6,动点P(x,0)在OB上运动(0<x<6),过点P作直线m与x轴垂直。
(1)求点C的坐标,并回答当x取何值时y1>y2?
(2)猜想△COB是什么三角形?并用所学的几何知识证明你的结论。
(3)设在△COB中位于直线m左侧部分的面积为S,求出S与x之间函数关系式?
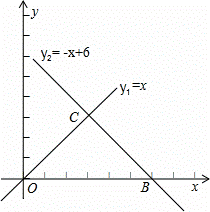
解:(1)由题意得: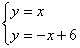 ,解得:
,解得: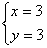 ,
,
∴点C的坐标为(3,3);
当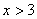 时
时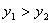 ;
;
(2)△COB是等腰直角三角形.
证明:∵直线BC的解析式为: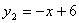 ,
,
∴B(6,0),
∵过点C作CD⊥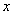 轴,垂足为D,点C(3,3),
轴,垂足为D,点C(3,3),
∴OD=CD,
∴∠COD=∠OCD=45°
又∵点B(6,0)
∴OB=6
∴BD=6-3=3
∴BD=CD=3
∴∠CBD=∠BCD=45°
∴∠COD=∠CBD=45°
∴∠OCB=180°—45°—45°=90°
∴△COB是等腰直角三角形;
(3)如图,过C作CD⊥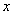 轴于点D,则D(3,0),
轴于点D,则D(3,0),
①当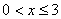 时,此时直线m左侧部分是△PQO,
时,此时直线m左侧部分是△PQO,
∵P(x,0),
∴OP=x,
而Q在直线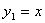 上,
上,
∴PQ=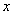 ,
,
∴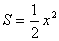 (0<
(0<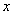 ≤3)
≤3)
 ②当3<
②当3<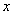 <6时,此时直线m左侧部分是四边形OPQC,
<6时,此时直线m左侧部分是四边形OPQC,
∵P(x,0),
∴OP=x,
∴PB=OB—OP=6—x,
而Q在直线上,
∴PQ=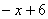 ,
,
∴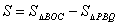
=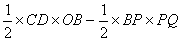
=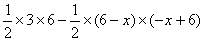
=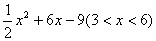

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.
 D.
D.
 = .
= .
 ,
, ,
, ,
, ,则小麦长势比较整齐的试验田是 .(填“甲”或者“乙”)
,则小麦长势比较整齐的试验田是 .(填“甲”或者“乙”)