题目内容
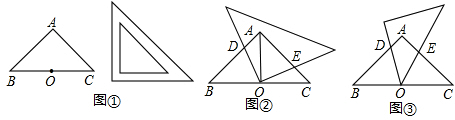
如图①,△ABC是一个等腰直角三角形纸板,点O为斜边BC的中点,腰长为14cm.将另一个等腰直角三角形的纸板的一个顶点放在点O处,与直角边AB、AC分别相交于D、E两点.
(1)如图②,当另一个等腰直角三角形纸板的直角顶点放在点O处时,连结AO;
①试说明△BOD≌△AOE.
②连结DE,若AD=6cm时,求DE的长度.
(2)如图③,当另一个等腰直角三角形纸板的锐角顶点放在点O处时,且AD=5cm时;试求DE的值.
(1)如图②,当另一个等腰直角三角形纸板的直角顶点放在点O处时,连结AO;
①试说明△BOD≌△AOE.
②连结DE,若AD=6cm时,求DE的长度.
(2)如图③,当另一个等腰直角三角形纸板的锐角顶点放在点O处时,且AD=5cm时;试求DE的值.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)①易证∠AOE=∠BOD,OA=OB,即可求证△BOD≌△AOE;
②连接DE,根据△BOD≌△AOE可以求得AE的长,根据勾股定理可以求得DE的长,即可解题;
(2)连接DE,AO,在AB中找到F点使得BF=AE,易证△OBF≌△OAE,可得OE=OF,BF=AE,∠BOF=∠AOE,即可证明△DOF≌△DOE,即可求得BD=AE+DE,再根据AD2+AE2=DE2,即可求得DE的长,即可解题.
②连接DE,根据△BOD≌△AOE可以求得AE的长,根据勾股定理可以求得DE的长,即可解题;
(2)连接DE,AO,在AB中找到F点使得BF=AE,易证△OBF≌△OAE,可得OE=OF,BF=AE,∠BOF=∠AOE,即可证明△DOF≌△DOE,即可求得BD=AE+DE,再根据AD2+AE2=DE2,即可求得DE的长,即可解题.
解答:(1)①证明:∵∠AOE+∠AOD=90°,∠AOD+∠BOD=90°,
∴∠AOE=∠BOD,
∵点O为等腰直角三角形ABC斜边BC的中点,
∴OA=OB,
∴在△BOD和△AOE中,
,
∴△BOD≌△AOE,(ASA);
②解:连接DE,

∵△BOD≌△AOE,
∴AE=BD=14-6=8,
∴DE=
=10;
(2)解:连接DE,AO,在AB中找到F点使得BF=AE,

∵O是等腰直角△ABC斜边BC中点,
∴AO=BO,∠B=∠CAO=45°,
∵在△OBF和△OAE中,
,
∴△OBF≌△OAE,(SAS)
∴OE=OF,BF=AE,∠BOF=∠AOE,
∵∠AOF+∠BOF=90°
∴∠AOF+∠AOE=90°,
∵∠DOE=45°,
∴∠DOF=45°,
∵在△DOF和△DOE中,
,
∴△DOF≌△DOE,(SAS)
∴DF=DE,
∴BD=BF+DF=AE+DE,
∵AD=5cm,AB=14cm,
∴BD=9cm,
∴DE+AE=9cm,
∵RT△ADE中,AD2+AE2=DE2,
∴DE=
.
∴∠AOE=∠BOD,
∵点O为等腰直角三角形ABC斜边BC的中点,
∴OA=OB,
∴在△BOD和△AOE中,
|
∴△BOD≌△AOE,(ASA);
②解:连接DE,

∵△BOD≌△AOE,
∴AE=BD=14-6=8,
∴DE=
| AE2+AD2 |
(2)解:连接DE,AO,在AB中找到F点使得BF=AE,

∵O是等腰直角△ABC斜边BC中点,
∴AO=BO,∠B=∠CAO=45°,
∵在△OBF和△OAE中,
|
∴△OBF≌△OAE,(SAS)
∴OE=OF,BF=AE,∠BOF=∠AOE,
∵∠AOF+∠BOF=90°
∴∠AOF+∠AOE=90°,
∵∠DOE=45°,
∴∠DOF=45°,
∵在△DOF和△DOE中,
|
∴△DOF≌△DOE,(SAS)
∴DF=DE,
∴BD=BF+DF=AE+DE,
∵AD=5cm,AB=14cm,
∴BD=9cm,
∴DE+AE=9cm,
∵RT△ADE中,AD2+AE2=DE2,
∴DE=
| 53 |
| 9 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,考查了直角三角形中勾股定理的运用,本题中求证△OBF≌△OAE和△DOF≌△DOE是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两个有理数a,b,|a|<|b|,并且a>0,b<0,则下列各式正确的是( )
| A、-a<b<a<-b |
| B、b<-a<a<-b |
| C、-a<-b<b<a |
| D、b<-a<-b<a |
在△ABC中,O为内心,∠A=80°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
 将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是( )
将三角形绕直线l旋转一周,可以得到如图所示的立体图形的是( )A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.当AD=2时,则AE的长为
如图,在△ABC中,AB=4,AC=3,D、E分别是AB、AC上的动点,在边AC上取一点E,使A、D、E三点组成的三角形与△ABC相似.当AD=2时,则AE的长为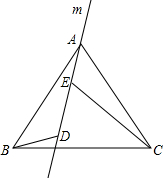 如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.
如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.