题目内容
17.(1)先化简,再求值:(x+2y)2-2(x+2y)(x-y)+(x-y)2,其中x=2015,y=-$\sqrt{2}$;(2)已知(x+2)(x2+ax+b)的积中不含有x的二次项和一次项,求a,b的值.
分析 (1)利用完全平方公式和整式的乘法计算,合并化简后代入求得答案即可;
(2)把式子展开,找出所有关于x的二次项,以及所有一次项的系数,令它们分别为0,解方程即可.
解答 解:(1)原式=x2+4xy+4y2-2x2-2xy+4y2+x2-2xy+y2
=9y2,
当x=2015,y=-$\sqrt{2}$时,
原式=18.
(2)∵(x+2)(x2+ax+b)=x3+ax2+bx+2x2+2ax+2b=x3+(a+2)x2+(b+2a)x+2b,
又∵积中不含x的二次项和一次项,
∴a+2=0,b+2a=0,
解得a=-2,b=4.
点评 此题考查整式的化简求值,掌握计算公式和计算方法是解决问题的关键.

练习册系列答案
相关题目
2.在x3-4x2+5x-k中,有一个因式为(x+2),则k的值为( )
| A. | -34 | B. | 34 | C. | 2 | D. | -2 |
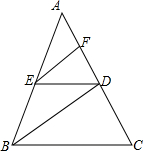 如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,
如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,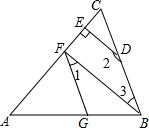 已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.
已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.