题目内容
对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得∠APB=60°,则称P为⊙C的关联点.已知点D( ,
, ),E(0,-2),F(
),E(0,-2),F( ,0).
,0).
(1) 当⊙O的半径为1时,① 在 点D,E,F中,
点D,E,F中,
⊙O的关联点是__________;② 过点F作直线l
交y轴正半轴于点G,使 ∠GFO=30°,若直线l
∠GFO=30°,若直线l
上的点P(m,n)是⊙O的关联点,求m的取值范围;
(2) 若线段EF上的所有点都是某个圆的关联点,求这个圆的半径r的取值范围.
 |
(1) ①D、E ;
 ②由题意可知,显然若P点是圆C距圆心最近的关联点,则这个点可在圆心,即这个距离为0.若P点是圆C距圆心最远的关联点,则点P到圆C的两条切线PA和PB之间所夹的角度为60°.由右图可知∠APB= 60°,则∠CPB= 30°,
②由题意可知,显然若P点是圆C距圆心最近的关联点,则这个点可在圆心,即这个距离为0.若P点是圆C距圆心最远的关联点,则点P到圆C的两条切线PA和PB之间所夹的角度为60°.由右图可知∠APB= 60°,则∠CPB= 30°,
连接 BC,则 PC=2BC=2r
∴若P点为圆C的关联点;则需点P 到圆心的距离d 满足 0≤d ≤2r .
 ∵∠GFO=30°,OF=
∵∠GFO=30°,OF= .
.
∴OG=2,∴G为l上最左边的⊙O的关联点.
在GF上取一点M使OM=2,
则为l上⊙O的关联点应在GM之间.
过M作MH⊥OF垂足为H
易得△OGM为等边三角形,在Rt△OMH中,∠MOH=30°∴OH=
即P(m,n)在线段GM上.∴0≤m≤
 (2) 若线段 EF 上的所有点都是某个圆的关联点,欲使这个圆的半径
(2) 若线段 EF 上的所有点都是某个圆的关联点,欲使这个圆的半径 最小,则这个圆的圆心应在线段EF的中点;设这个点为I.
最小,则这个圆的圆心应在线段EF的中点;设这个点为I.
∵EF= =4
=4
∴IF=2,由前面计算知⊙I的半径为1,
故若线段EF上的所有点都是某个圆的关联点,
这个圆的半径r的取值范围为r≥1.

如图,在△ABC中,分别以点A和点B为圆心,大于的  AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )。
 |
A、7 B、14 C、17 D、20
为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机调查了部分参赛同学的成绩,整理并制作图表如下.
 |
请根据以上图表提供的信息,解答下列问题:
(1) 求出本次调查的样本容量;
(2) 求出表中m与n的值;
(3) 补全频数分布直方图;
(4) 参加比赛的小聪说,他的比赛成绩是所在抽查同学成绩的中位数,据此推测他的成绩落在哪一个分数段内?
(5) 如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是多少?

 统计图;
统计图; 3)在成绩为19分的同学中有三人(两男一女),20分的同学中有两人(一男一女)共5位同学的双跳水平很高,现准备从他们中选出两位同学给全年级同学作示范,请用树状图或列表法求刚好抽得两位男生的概率.
3)在成绩为19分的同学中有三人(两男一女),20分的同学中有两人(一男一女)共5位同学的双跳水平很高,现准备从他们中选出两位同学给全年级同学作示范,请用树状图或列表法求刚好抽得两位男生的概率. B.
B. C.
C. D.
D.
 ,
, 从
从 中随机取一个值,
中随机取一个值, 从
从 中随机取一个值,则该一次函数的图象经过二、三、四象
中随机取一个值,则该一次函数的图象经过二、三、四象 限的概率为
限的概率为 B.
B.  C.
C.  D.
D. 
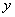 =
= 分别与
分别与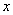 轴,
轴, 两点,点
两点,点 是
是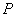 为圆心,3为半径作
为圆心,3为半径作 .
. ,若
,若 ,试判断
,试判断
