题目内容
如图,在平面直角坐标系中,直线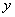 =
= 分别与
分别与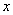 轴,
轴,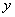 轴相交于
轴相交于 两点,点
两点,点 是
是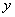 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以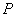 为圆心,3为半径作
为圆心,3为半径作 .
.
(1)连结 ,若
,若 ,试判断
,试判断 与
与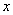 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当 为何值时,以
为何值时,以 与直线
与直线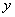 =
= 的两个交点和圆心
的两个交点和圆心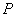 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
 |  | ||
解:(1) 与
与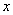 轴相切.
轴相切.
直线 与
与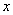 轴交于
轴交于 ,与
,与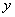 轴交于
轴交于 ,
,
 ,…
,…
由题意, .
.
在 中,
中, ,
,
 等于
等于 的半径,
的半径, 与
与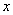 轴相切.
轴相切.
(2)设 与直线交于
与直线交于 两点,连结
两点,连结 .
.
当圆心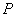 在线段
在线段 上时,作
上时,作 于
于 .
.
 为正三角形,
为正三角形,

 ,
,

∵ ,∴AB=
,∴AB=
∴
 .
.
当圆心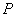 在线段
在线段 延长线上时,同理可得
延长线上时,同理可得
 ,
,
当 或
或 时,以
时,以 与直线的两个交点和圆心
与直线的两个交点和圆心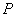 为顶点的三角形是正三角形.
为顶点的三角形是正三角形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (
( )的图象如图所示,对称轴是直线
)的图象如图所示,对称轴是直线 ,有下列结论:①
,有下列结论:① ;②
;② ;③
;③ ;④
;④
 .其中正确结论的个数是( ).
.其中正确结论的个数是( ).
 ,
, ,0).
,0). 点D,E,F中,
点D,E,F中,
 的解集是______________.
的解集是______________. 、
、 、
、 、
、 在同一条直线上,
在同一条直线上, ,
, ,
, .
. .
.

 为每平方米商品房成交价格,单位:万元/平方米).
为每平方米商品房成交价格,单位:万元/平方米).