题目内容
如图①,如果A1、A2、A3、A4把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形4个;如图②,如果A1、A2、A3、A4、A5、A6把圆周六等分,则以A1、A2、A3、A4、A5、A6为点的直角三角形有12个;
如果A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有 个.

如果A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有

考点:规律型:图形的变化类,圆周角定理
专题:
分析:根据圆周角定理找到直径所对的圆周角是直角,然后由一条直径所对的直角数来寻找规律.
解答: 解:由圆周角定理知,直径所对的圆周角是直角.
解:由圆周角定理知,直径所对的圆周角是直角.
∴当A1、A2、A3、A4把圆周四等分时,该圆中的直径有A1A3,A2A4两条,
∴①当以A1A3为直径时,有两个直角三角形;
②当以A2A4为直径时,有两个直角三角形;
∴如果A1、A2、A3、A4把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形有(4÷2)×(4-2)=4个;
当A1、A2、A3、A4、A5、A6把圆周六等分,则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有(6÷2)×(6-2)=12个;
当A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有(2n÷2)×(2n-2)=2n(n-1)个.
故答案是:2n(n-1).
 解:由圆周角定理知,直径所对的圆周角是直角.
解:由圆周角定理知,直径所对的圆周角是直角.∴当A1、A2、A3、A4把圆周四等分时,该圆中的直径有A1A3,A2A4两条,
∴①当以A1A3为直径时,有两个直角三角形;
②当以A2A4为直径时,有两个直角三角形;
∴如果A1、A2、A3、A4把圆周四等分,则以A1、A2、A3、A4为顶点的直角三角形有(4÷2)×(4-2)=4个;
当A1、A2、A3、A4、A5、A6把圆周六等分,则以A1、A2、A3、A4、A5、A6为顶点的直角三角形有(6÷2)×(6-2)=12个;
当A1、A2、A3、…A2n把圆周2n等分,则以A1、A2、A3、…A2n为顶点的直角三角形有(2n÷2)×(2n-2)=2n(n-1)个.
故答案是:2n(n-1).
点评:本题考查了圆周角定理:直径所对的圆周角是直角.解答该题是关键是根据直径的条数、顶点的个数来寻找规律.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
下列各数中是无理数的是( )
1.
,-
,
,
π,0.020020002…,-2,
-1.
1.
| • |
| 3 |
| • |
| 4 |
| 12 |
| 3 | 64 |
| 1 |
| 2 |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
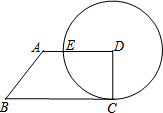 如图,已知直角梯形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E,若
如图,已知直角梯形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E,若
 如图,已知△ABC,∠ACB的平分线CD交AB于点D,DE∥BC交AC于点E.如果EC=2AE,AC=5,则DE=
如图,已知△ABC,∠ACB的平分线CD交AB于点D,DE∥BC交AC于点E.如果EC=2AE,AC=5,则DE= 关于x的不等式3x-2a≤-2的解集如图,则a=
关于x的不等式3x-2a≤-2的解集如图,则a= 2013年中国长6625消夏节活动中,参加净月潭瓦萨国际森林徒步节的志愿者的年龄分布如图,这些志愿者年龄的众数是
2013年中国长6625消夏节活动中,参加净月潭瓦萨国际森林徒步节的志愿者的年龄分布如图,这些志愿者年龄的众数是