题目内容
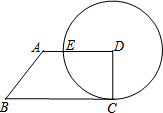 如图,已知直角梯形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E,若
如图,已知直角梯形ABCD中,AD∥BC,∠C=90°,∠B=45°,以D为圆心,DC为半径的圆交AD于点E,若 |
| CE |
| 3 |
考点:直线与圆的位置关系,直角梯形,弧长的计算
专题:
分析:首先利用弧长公式求得CD的长,然后过D作DF⊥BA,交线段BA延长线于点F,利用锐角三角函数求得线段DF的长,比较后即可确定答案.
解答: 解∵AD∥BC,∠C=90°
解∵AD∥BC,∠C=90°
∴∠D=180°-∠C=90°,
∴
的长=
πR=
πCD
∴
πCD=π,
∴CD=2,
过D作DF⊥BA,交线段BA延长线于点F,
∵AD∥BC,
∴∠DAF=∠B=45°,
在RT△DAF中
sin∠DAF=
,
∴
=
∴DF=
>2,
∴AB与⊙D没有交点.
 解∵AD∥BC,∠C=90°
解∵AD∥BC,∠C=90°∴∠D=180°-∠C=90°,
∴
 |
| CE |
| 90 |
| 180 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴CD=2,
过D作DF⊥BA,交线段BA延长线于点F,
∵AD∥BC,
∴∠DAF=∠B=45°,
在RT△DAF中
sin∠DAF=
| DF |
| DA |
∴
| DF | ||
2
|
| ||
| 2 |
∴DF=
| 6 |
∴AB与⊙D没有交点.
点评:本题考查了直角梯形、弧长的计算、直线与圆的位置关系等知识,知识点较多,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,P是⊙O外一点,PA是⊙O的切线,PO=13,PA=12,则⊙O的周长为
如图,P是⊙O外一点,PA是⊙O的切线,PO=13,PA=12,则⊙O的周长为