题目内容
11.代数式-$\frac{3x}{2}$,$\frac{4}{x-y}$,$\frac{x+y}{2x}$,$\frac{{x}^{2}+1}{π}$,$\frac{7}{8}$,$\frac{5b}{3a}$中是分式的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据分式的定义进行解答即可,即分母中含有未知数的式子叫分式.
解答 解:在代数式-$\frac{3x}{2}$,$\frac{4}{x-y}$,$\frac{x+y}{2x}$,$\frac{{x}^{2}+1}{π}$,$\frac{7}{8}$,$\frac{5b}{3a}$中是分式的有$\frac{4}{x-y}$,$\frac{x+y}{2x}$,$\frac{5b}{3a}$,共3个.
故选B.
点评 本题主要考查分式的定义,注意π不是字母,是常数,所以$\frac{{x}^{2}+1}{π}$不是分式,是整式.

练习册系列答案
相关题目
6.在平面直角坐标系中,已知一次函数y=kx+b的图象经过二、三、四象限,则下列结论正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0. |
20.现用190张铁皮制作一批盒子,每张铁皮可做8个盒身或做22个盒底,而一个盒身和两个盒底配成一个完整的盒子.问用多少张白铁皮制盒身、多少张白铁皮制盒底,可以使盒身和盒底正好配套.设用x张铁皮做盒身,y张铁皮做盒底,可以使盒身与盒底正好配套,则可列方程是( )
| A. | $\left\{\begin{array}{l}{x+2y=190}\\{8x=22y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=190}\\{2×8x=22y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+2y=190}\\{2×8x=22y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=190}\\{2×22y=8x}\end{array}\right.$ |
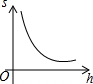
 如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )
如图,已知点P是y轴正半轴上任意一点,过点P作x轴的平行线交抛物线y=x2于点C,D(点C在点D的右边),过点C作CB⊥x轴于点B,过点D作DA⊥x轴于点A,分别以OA,OB为直径作半圆.设点P的纵坐标为h,图中阴影部分的面积为s,则s与h之间的函数关系的图象大致是( )