题目内容
1．
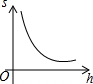如图，已知点P是y轴正半轴上任意一点，过点P作x轴的平行线交抛物线y=x2于点C，D（点C在点D的右边），过点C作CB⊥x轴于点B，过点D作DA⊥x轴于点A，分别以OA，OB为直径作半圆．设点P的纵坐标为h，图中阴影部分的面积为s，则s与h之间的函数关系的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由点P的纵坐标为h，CD∥x轴，于是得到点D，C的纵坐标为h，由于点C，D在抛物线y=x2上，于是得到点D，C的横坐标分别为-$\sqrt{h}$，$\sqrt{h}$，求出OA=OB=$\sqrt{h}$，根据圆的面积公式列方程即可得到结论．
解答 解：∵点P的纵坐标为h，CD∥x轴，
∴点D，C的纵坐标为h，
∵点C，D在抛物线y=x2上，
∴点D，C的横坐标分别为-$\sqrt{h}$，$\sqrt{h}$，
∴OA=OB=$\sqrt{h}$，
∴阴影部分的面积s=（$\frac{\sqrt{h}}{2}$）2π，
∴s=$\frac{π}{4}$h，
∴s是h的正比例函数．
故选B．
点评 本题考查了动点问题的函数图象，圆的面积的计算，图象上点的坐标的求法，正确的识图是解题的关键．
练习册系列答案
相关题目
7．
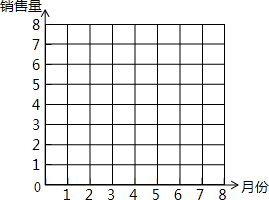甲、乙两人在某公司做见习推销员，推销“小天鹅”洗衣机，他们在1～8月份的销售情况如下表所示：
（1）在图给出的图形中，绘制甲、乙两人这8个月的销售量的折线图；（甲用实线，乙用虚线）
（2）请根据（1）中的折线统计图，写出2条关于甲、乙两人在这8个月中的销售状况的信息．
甲、乙两人在某公司做见习推销员，推销“小天鹅”洗衣机，他们在1～8月份的销售情况如下表所示：| 月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
| 甲的销售量（单位：台） | 7 | 8 | 6 | 7 | 6 | 6 | 7 | 7 |
| 乙的销售量（单位：台） | 5 | 6 | 5 | 6 | 7 | 7 | 8 | 9 |
（2）请根据（1）中的折线统计图，写出2条关于甲、乙两人在这8个月中的销售状况的信息．
6．下列说法中，正确的是（ ）
| A． | 单项式4a+$\frac{1}{b}$m的次数是0 | |
| B． | $\frac{1}{x}$是整式 | |
| C． | -$\frac{1}{4}$不是单项式 | |
| D． | 单项式-$\frac{{{2^3}mn}}{8}$的系数是-1，次数是2 |