题目内容
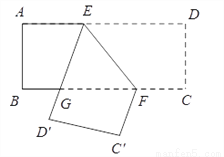
如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点G,点D,C分别落在C?,D?的位置上,若∠EFG = 55°,则∠GFC?= ________°.
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
如图,把一张长方形ABCD的纸片沿EF折叠后,ED与BC的交点G,点D,C分别落在C?,D?的位置上,若∠EFG = 55°,则∠GFC?= ________°.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案