将抛物线y=x2向下平移2个单位长度.再向右平移1个单位长度后.得到的抛物线的表达式为( )A．y=(x-1)2+2B．y=(x+1)2-2C．y=(x-2)2-1D．y=(x-1)2-2 题目和参考答案——青夏教育精英家教网—

题目内容

2．将抛物线y=x²向下平移2个单位长度，再向右平移1个单位长度后，得到的抛物线的表达式为（　　）

A．

y=（x-1）²+2

B．

y=（x+1）²-2

C．

y=（x-2）²-1

D．

y=（x-1）²-2

分析先利用顶点式得到抛物线y=x²的顶点坐标为（0，0），再根据点利用的规律得到点（0，0）平移后所得对应点的坐标为（1，-2），然后根据顶点式写出平移后抛物线的解析式．

解答解：抛物线y=x²的顶点坐标为（0，0），点（0，0）向下平移2个单位，再向右平移1个单位所得对应点的坐标为（1，-2），所以所得到的抛物线的解析式是y=（x-1）²-2．
故选D．

点评本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．

练习册系列答案

相关题目

（x³）²=x⁵

x²+x³=x⁵

13．把4m的木料锯成六段，制成如图所示的“目”字型窗户，用于新建鸡舍；若用x（m）表示横料AB的长，y（m²）表示窗户的面积，则y与x之间的函数关系式为y=-2x²+2x，当x=0.5m时窗户面积最大．

10．已知线段AB=2cm，延长线段AB到C，使BC=4cm，D为线段AC的中点，则线段BD的长为1cm．

17．

园艺师从土地上收集了许多大理石的边角料，准备给公共绿地的通道铺地面，其中最多的一种边角材料形状如图所示，你能否用这种边角料铺满地面？如果能，请设计出至少两种方案．

7．

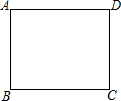如图，某广场为矩形ABCD，现准备在广场的内部修建照明灯，要求照明灯0到广场的两个人口A，D的距离相等，且到AB，BC两边的距离相等．
（1）用直尺和圆规作出点0的位置．（不写作法，保留作图痕迹）
（2）已知AB=320m，AD=400m，求0B的距离．

14．

如果将一副三角板按如图方式摆放，使∠1=15°，那么∠AOB的度数是（　　）

3．

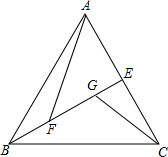如图，△ABC是等边三角形，BE⊥AC于E，点F、G在BE上（BF＜BG），连接AF，CG，CG²=GF•GB，
（1）求证：∠AFE=∠BCG；
（2）过点F作直线CG的垂线，垂足为H，M为AB的中点，连接MH，探究MH与BF之间的数量关系，并证明你的结论．

试题分类