题目内容
14.解方程:(1)x2-3x-2=0
(2)(x-3)2=4x(x-3)
(3)$\frac{x}{x-2}$=$\frac{3(x-2)}{x}$+2.
分析 (1)求出b2-4ac的值,再代入公式求出即可;
(2)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(3)设$\frac{x}{x-2}$=y,则原方程化为y=$\frac{3}{y}$+2,求出y,再代入求出x即可.
解答 (1)x2-3x-2=0,
b2-4ac=(-3)2-4×1×(-2)=17,
x=$\frac{3±\sqrt{17}}{2}$,
x1=$\frac{3+\sqrt{17}}{2}$,x2=$\frac{3-\sqrt{17}}{2}$;
(2)(x-3)2=4x(x-3),
(x-3)2-4x(x-3)=0,
(x-3)(x-3-4x)=0,
x-3=0,x-3-4x=0,
x1=3,x2=-1;
(3)设$\frac{x}{x-2}$=y,则原方程化为:y=$\frac{3}{y}$+2,
解得:y=3或-1,
当y=3时,$\frac{x}{x-2}$=3,
解得:x=3,
当y=-1时,$\frac{x}{x-2}$=-1,
解得:x=1,
经检验x=3和x=1都是原方程的解,
即原方程的解为x1=3,x2=1.
点评 本题考查了解一元二次方程和分式方程的应用,能选择适当的方法解一元二次方程是解(1)、(2)题的关键,能正确换元是解(3)的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
4.32015+5除以32012-1,所得的余数是( )
| A. | 313-1 | B. | 311-1 | C. | 32 | D. | 8 |
9. 如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )
如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )
 如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )
如图,△ABC中,∠C=90°,且c=2a,则sinB的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.下列式子中成立的是( )
| A. | (-2)2>-32 | B. | -0.3<-$\frac{1}{3}$ | C. | -$\frac{4}{5}$<-$\frac{7}{6}$ | D. | -$\frac{10}{9}$>-$\frac{9}{10}$ |
6.平面直角坐标系中,⊙O是以原点O为圆心,4为半径的圆,则点A(2,-2)的位置在( )
| A. | ⊙O内 | B. | ⊙O上 | C. | ⊙O外 | D. | 不能确定 |
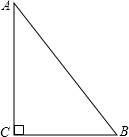 如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.