题目内容
7.求|x-1|+|x-2|+…+|x-100|+|x|+|x+1|+…+|x+100|的最小值.分析 根据绝对值的性质,两端的数距离远点越近,则所求的值越小,然后进行解答即可.
解答 解:∵共有100+100+1=201个数,
∴x=0时,两边的数关于|x|对称,此时的和最小,
此时|x-1|+|x-2|+…+|x-100|+|x|+|x+1|+…+|x+100|
=(1-x)+(2-x)…+(100-x)+x+(x+1)+(x+1)+…+(x+100)
=2×(1+2+3+4+…+100)
=2×$\frac{100×(1+100)}{2}$
=10100.
故|x-1|+|x-2|+…+|x-100|+|x|+|x+1|+…+|x+100|的最小值是10100.
点评 本题考查了绝对值的性质,判断出当x=0时,代数式的和最小是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.
如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.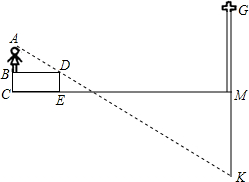 在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.
在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.