题目内容
12．已知，在△ABC中，D，E，F分别是边BC、CA、AB的中点．求证：四边形AFDE的周长等于AB+AC．分析 作出图形，根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=$\frac{1}{2}$AB=BF，DF=$\frac{1}{2}$AC=CE，然后整理即可得证．
解答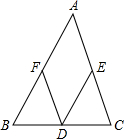 
证明：如图，∵D，E，F分别是边BC、CA、AB的中点，
∴DE、DF都是△ABC的中位线，
∴DE=$\frac{1}{2}$AB=BF，DF=$\frac{1}{2}$AC=CE，
∴四边形AFDE的周长=AF+DF+DE+AE=AF+BF+CE+AE=AB+AC，
即：四边形AFDE的周长等于AB+AC．
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半，是基础题，熟记定理是解题的关键，作出图形更形象直观．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
