题目内容
7．如果在0，1，2，3这四个数中任取两数m，n，则二次函数y=（x-m）2+n的顶点不在坐标轴上的概率为$\frac{1}{2}$．分析 画树状图展示所有12种等可能的结果数，再利用二次函数的性质得到二次函数y=（x-m）2+n的顶点坐标为（m，n），然后根据坐标轴上点的坐标特征可判断顶点不在坐标轴上的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有12种等可能的结果数，其中二次函数y=（x-m）2+n的顶点（m，n）不在坐标轴上的结果数为6，
则二次函数y=（x-m）2+n的顶点不在坐标轴上的概率为$\frac{6}{12}$=$\frac{1}{2}$；
故答案为：$\frac{1}{2}$．
点评 本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
练习册系列答案
相关题目
一副三角板如图摆放，∠1=65°，则∠2=65度．
如图所示的程序中，要使输出值y大于70，则输入的最小正整数x是21．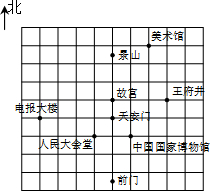
“四个一”活动自2014年9月启动至今，北京市已有60万中小学生参观了天安门广场的升旗仪式．下图是利用平面直角坐标系画出的天安门广场周围的景点分布示意图．如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示故宫的点的坐标为（0，1），表示中国国家博物馆的点的坐标为（1，-1），那么表示人民大会堂的点的坐标是（-1，1）．
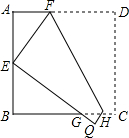如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长是$\frac{9}{4}$cm．