题目内容
18.若关于x的一元一次不等式为(2-m)x|x-3|-6>0,则点P(1-m,m-1)在第二象限.分析 根据一元一次不等式的定义列方程求出m的值,再求出点P的坐标,然后根据各象限内点的坐标特征解答.
解答 解:∵(2-m)x|m-3|-6>0是一元一次不等式,
∴|m-3|=1且2-m≠0,
∴m-3=1或m-3=-1且m≠2,
解得m=4,
所以,点P的坐标为(-3,3),
∴点P(1-m,m-1)在第二象限.
故答案为:二.
点评 本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
10. 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
8.我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
| A. | 2.5×10-5 | B. | 2.5×105 | C. | 2.5×10-6 | D. | 2.5×106 |
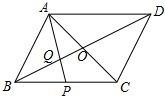 如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$.
如图,在?ABCD中,对角线AC,BD相交于点O,P是BC边中点,AP交BD于点Q.则$\frac{OQ}{OB}$的值为$\frac{1}{3}$.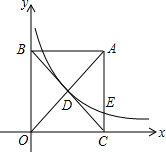 如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x.
如图,已知矩形ABOC的对角线相交于点D,O为坐标原点,OC在x轴的正半轴上,双曲线y=$\frac{k}{x}$(k>0)经过点D,与边AC相交于点E.若OC2=CE•CA,则直线OA的解析式为y=2x.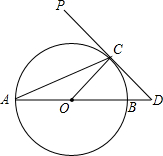 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.