题目内容
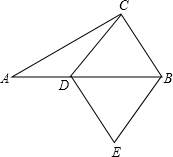 如图,在△ABC中,BC=8,AC=15,AB=17,D为边AB上一点,CD=CB,以CD,CB为边作菱形CDEB.
如图,在△ABC中,BC=8,AC=15,AB=17,D为边AB上一点,CD=CB,以CD,CB为边作菱形CDEB.(1)求证:△ABC是直角三角形;
(2)求AD的长.
考点:菱形的性质,勾股定理,勾股定理的逆定理
专题:
分析:(1)利用勾股定理的逆定理,可判断结论;
(2)根据△ABC的面积表达式求出CH,继而利用勾股定理求出BH,从而可求AD.先求出
(2)根据△ABC的面积表达式求出CH,继而利用勾股定理求出BH,从而可求AD.先求出
解答:证明:(1)在△ABC中,∵AC2+BC2=82+152=289=172,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
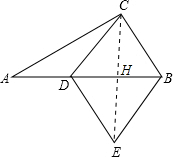 (2)连接CE交AB于点H,
(2)连接CE交AB于点H,
在菱形CDEB中,CE⊥BD且HD=HB,CD=CB,
由S△ABC=
AB×CH=
AC×BC,
∴CH=
,
在Rt△BCH中,HB=
=
=
,
∴AD=AB-2BH=
.
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
 (2)连接CE交AB于点H,
(2)连接CE交AB于点H,在菱形CDEB中,CE⊥BD且HD=HB,CD=CB,
由S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=
| 120 |
| 17 |
在Rt△BCH中,HB=
| BC2-HC2 |
82-(
|
| 64 |
| 17 |
∴AD=AB-2BH=
| 161 |
| 17 |
点评:本题考查了菱形的性质、勾股定理及三角形的面积,解答本题的关键是熟练掌握勾股定理的逆定理、菱形的性质.

练习册系列答案
相关题目
 如图,平面直角坐标中,点A(1,2),将AO绕点A逆时针旋转90°,点O的对应B点恰好落在双曲线y=
如图,平面直角坐标中,点A(1,2),将AO绕点A逆时针旋转90°,点O的对应B点恰好落在双曲线y=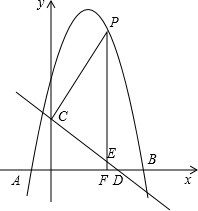 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-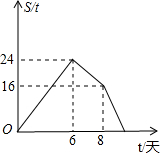 春耕期间,某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是
春耕期间,某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是