题目内容
9.已知x,y满足$\frac{x}{y}$=5,求分式$\frac{{x}^{2}-2xy+3{y}^{2}}{4{x}^{2}+5xy-6{y}^{2}}$的值.分析 首先根据$\frac{x}{y}$=5得x=5y,再代入分式$\frac{{x}^{2}-2xy+3{y}^{2}}{4{x}^{2}+5xy-6{y}^{2}}$可达到消元的目的,然后约分即可.
解答 解:∵$\frac{x}{y}$=5,
∴x=5y,
把x=5y代入$\frac{{x}^{2}-2xy+3{y}^{2}}{4{x}^{2}+5xy-6{y}^{2}}$=$\frac{(5y)^{2}-2•5y•y+3{y}^{2}}{4×(5y)^{2}+5×5y•y-6{y}^{2}}$=$\frac{18{y}^{2}}{119{y}^{2}}$=$\frac{18}{119}$.
点评 此题主要考查了分式的值,关键是正确掌握代入消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.某股票经纪人给他的投资者列出下表,说明投资人的盈利净赚情况:(单位:元)
请你计算一下,投资者到底赔了还是赚了?赔或赚了多少元?
| 股票名称 | 每股净赚(元) | 股数 |
| 天河 | +4 | 500 |
| 北斗 | -1.5 | 1000 |
| 白马 | +3 | 1000 |
| 海潮 | -2 | 500 |

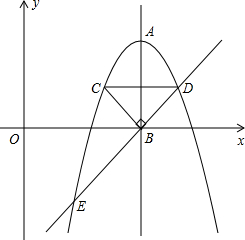 如图,抛物线y=-x2+12x-30的顶点为A,对称轴AB与x轴交于点B.在x轴上方的抛物线上有C、D两点,它们关于AB对称,并且C点在对称轴的左侧,CB⊥DB.
如图,抛物线y=-x2+12x-30的顶点为A,对称轴AB与x轴交于点B.在x轴上方的抛物线上有C、D两点,它们关于AB对称,并且C点在对称轴的左侧,CB⊥DB.