题目内容
20．若x+y=2，xy=-5，求下列各式的值：（1）$\frac{1}{x}$+$\frac{1}{y}$；
（2）$\frac{x}{y}$+$\frac{y}{x}$．
分析 （1）先通分，然后利用整体代入的方法计算；
（2）先通分，再利用完全平方公式变形得到$\frac{（x+y）^{2}-2xy}{xy}$，然后利用整体代入的方法计算．
解答 解：（1）原式=$\frac{x+y}{xy}$=$\frac{2}{-5}$=-$\frac{2}{5}$；
（2）原式=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{（x+y）^{2}-2xy}{xy}$=$\frac{{2}^{2}-2×（-5）}{-5}$=-$\frac{14}{5}$．
点评 本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．
练习册系列答案
相关题目
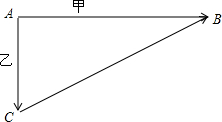甲、乙两只渔船同时从一渔港（A）出发，甲船向正东方向航行，速度是8海里/小时，乙船向正南方向航行，速度是6海里/小时，2小时后，甲船到达B处，乙船到达C处．
15．“比a的$\frac{3}{2}$倍大1的数”用式子表示为（ ）
| A． | $\frac{2}{3}$a+1 | B． | $\frac{3}{2}$a+1 | C． | $\frac{5}{2}$a | D． | $\frac{3}{2}$a-1 |
已知：如图，点0在线段AD上，A0=AB，DO=DC，且OB⊥OC．求证：AB∥DC．