题目内容
 已知E为?ABCD外的一点,∠AEC=∠BED=90°,求证:四边形ABCD是矩形.
已知E为?ABCD外的一点,∠AEC=∠BED=90°,求证:四边形ABCD是矩形.考点:矩形的判定
专题:证明题
分析:连接EO,首先根据平行四边形的性质可得AO=CO,BO=DO,即O为BD和AC的中点,在Rt△AEC中EO=
AC,在Rt△EBD中,EO=
BD,进而得到AC=BD,再根据对角线相等的平行四边形是矩形可证出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:连接EO,
证明:连接EO,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
在Rt△EBD中,
∵O为BD中点,
∴EO=
BD,
在Rt△AEC中,∵O为AC中点,
∴EO=
AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
 证明:连接EO,
证明:连接EO,∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
在Rt△EBD中,
∵O为BD中点,
∴EO=
| 1 |
| 2 |
在Rt△AEC中,∵O为AC中点,
∴EO=
| 1 |
| 2 |
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评:此题主要考查了矩形的判定,关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
若
+(y-1)2=0,则x-y=( )
| x+2y |
| A、1 | B、2 | C、3 | D、-3 |
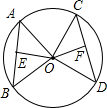 如图,AB,CD是⊙O的两条弦,OE⊥AB于点E,OF⊥CD于点F,如果OE>OF,那么AB和CD有什么关系,为什么?
如图,AB,CD是⊙O的两条弦,OE⊥AB于点E,OF⊥CD于点F,如果OE>OF,那么AB和CD有什么关系,为什么? 如图,已知矩形ABCD的周长为16,四个正方形的面积和为68,求矩形ABCD的面积.
如图,已知矩形ABCD的周长为16,四个正方形的面积和为68,求矩形ABCD的面积. 如图,矩形ABCD的周长为24cm,两条对角线相交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,求△CDE的周长.
如图,矩形ABCD的周长为24cm,两条对角线相交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,求△CDE的周长.