题目内容
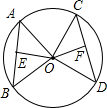如图，AB，CD是⊙O的两条弦，OE⊥AB于点E，OF⊥CD于点F，如果OE＞OF，那么AB和CD有什么关系，为什么？考点：垂径定理,勾股定理
专题：几何图形问题
分析：根据勾股定理计算出AE、CF的长度表达式，再根据垂径定理计算出AB、CD的表达式，比较即可．
解答：解：AB＜CD．
∵OE⊥AB，OF⊥CD，
∴AE=EB，CF=DF，
∴AE=
，
∴CF=
，
∵OE＞OF，
∴AE＜CF，
∴2AE＜2CF，
∴AB＜CD．
∵OE⊥AB，OF⊥CD，
∴AE=EB，CF=DF，
∴AE=
| AO2-OE2 |
∴CF=
| OC2-OF2 |
∵OE＞OF，
∴AE＜CF，
∴2AE＜2CF，
∴AB＜CD．
点评：本题考查了垂径定理和勾股定理，在圆中，两定理伴随出现，要联合应用，事半功倍．
练习册系列答案
相关题目
正方形的面积是4，则它的对角线长是（ ）
| A、2 | ||
B、
| ||
C、2
| ||
| D、4 |
已知E为?ABCD外的一点，∠AEC=∠BED=90°，求证：四边形ABCD是矩形．