题目内容
如图，已知矩形ABCD的周长为16，四个正方形的面积和为68，求矩形ABCD的面积．考点：一元二次方程的应用
专题：几何图形问题,整体思想
分析：设矩形的长AB为x，则宽AD为（8-x），故矩形的面积为x（8-x），根据四个正方形的面积之和为68建立方程求出其解即可．
解答：解：设矩形的长AB为x，则宽AD为（8-x），由题意，得
2x2+2（8-x）2=68，
2x2+2（64-16x+x2）=68，
2x2+128-32x+2x2=68，
∴4x2-32x=-60，
∴x2-8x=-15，
∴8x-x2=15
∴x（8-x）=15，
∵矩形的面积为x（8-x），
∴矩形ABCD的面积为15．
2x2+2（8-x）2=68，
2x2+2（64-16x+x2）=68，
2x2+128-32x+2x2=68，
∴4x2-32x=-60，
∴x2-8x=-15，
∴8x-x2=15
∴x（8-x）=15，
∵矩形的面积为x（8-x），
∴矩形ABCD的面积为15．
点评：本题考查了列一元二次方程解实际问题的运用，矩形的面积公式的运用，整体数学思想的运用，解答时根据四个正方形的面积和为68建立方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
不能判断四边形ABCD为平行四边形的题设是（ ）
| A、AB平行且等于CD |
| B、AB=AD，∠B=∠D |
| C、AB=CD，AD=BC |
| D、∠A=∠C，∠B=∠D |
在Rt△ABC中，∠C=90°，∠B=45°，D为BC上一点，且BD=2
已知E为?ABCD外的一点，∠AEC=∠BED=90°，求证：四边形ABCD是矩形．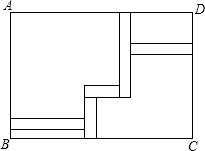
学校的课外生物小组的实验园地是一块长35米，宽26米的长方形，为了便于行走和管理，现要在中间修同样宽的到路，路宽均为a米，余下的作为种植面积，求种植面积是多少？