题目内容
17.已知AB为⊙O的一条弦,且长度与半径相等,则$\widehat{AB}$所对的圆周角的度数为30°或150°.分析 根据弦长等于半径,得这条弦和两条半径组成了等边三角形,则弦所对的圆心角是60°,要计算它所对的圆周角,应考虑两种情况:当圆周角的顶点在优弧上时,则根据圆周角定理,得此圆周角是30°;当圆周角的顶点在劣弧上时,则根据圆内接四边形的对角互补,得此圆周角是150°.
解答 解:根据题意,∵弦AB与两半径组成等边三角形,
∴AB所对的圆心角=60°,
①圆周角在优弧上时,圆周角=30°,
②圆周角在劣弧上时,圆周角=180°-30°=150°.
∴圆周角的度数为30°或150°.
故答案为:30°或150°.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
9.若X=2$\sqrt{2}$+$\sqrt{20}$,Y=3$\sqrt{3}$+$\sqrt{7}$,Z=$\sqrt{6}$+2$\sqrt{7}$,则( )
| A. | X最小 | B. | Y最小 | C. | Z最小 | D. | X、Y、Z一样大 |
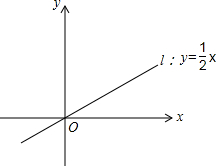 如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.
如图,直线l:y=$\frac{1}{2}$x,若直线上有一点A,A在第一象限,且OA=$\sqrt{5}$.