��Ŀ����
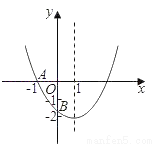
��ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2���ͣ�0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x=1�����н��ۣ���abc��0 ��4a+2b+c��0 ��4ac��b2��8a ��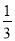 ��a��
��a��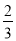 ��b��c�����к�������ȷ���۵�ѡ���ǣ�������
��b��c�����к�������ȷ���۵�ѡ���ǣ�������
A. �٢� B. �٢ۢ� C. �ڢܢ� D. �٢ۢܢ�
 D
������������������١ߺ������ڷ������ϣ���a��0���߶Գ�����y���Ҳ࣬��ab��ţ�����������y�ύ����y�Ḻ���ᣬ��c��0����abc��0���ʢ���ȷ���ڡ�ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����ͼ����x�����һ������Ϊ��3��0�����൱x=2ʱ��y��0����4a+2b+c��0���ʢڴ��ۡ�ͼ����x�ύ�ڵ�A����1��0�����൱x=��1ʱ��y= =0����a��b+c=0����a=b��c...
D
������������������١ߺ������ڷ������ϣ���a��0���߶Գ�����y���Ҳ࣬��ab��ţ�����������y�ύ����y�Ḻ���ᣬ��c��0����abc��0���ʢ���ȷ���ڡ�ͼ����x�ύ�ڵ�A����1��0�����Գ���Ϊֱ��x=1����ͼ����x�����һ������Ϊ��3��0�����൱x=2ʱ��y��0����4a+2b+c��0���ʢڴ��ۡ�ͼ����x�ύ�ڵ�A����1��0�����൱x=��1ʱ��y= =0����a��b+c=0����a=b��c...
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д���һ����n���ε�ÿ���ڽ�Ϊ144�㣬�������n���ε����жԽ��ߵ������ǣ�������
A. 7 B. 10 C. 35 D. 70
 C
������������n���ε�ÿ���ڽ�Ϊ144���϶�����ڽǺ�ʽ�����ɵó�����n��һԪһ�η��̣��ⷽ�̼������n��ֵ����������м��ɵó����ۣ�
��������
��һ����n���ε�ÿ���ڽ�Ϊ144�㣬
��144n=180����n��2������ã�n=10��
�����n���ε����жԽ��ߵ������ǣ�==35��
��ѡC��
C
������������n���ε�ÿ���ڽ�Ϊ144���϶�����ڽǺ�ʽ�����ɵó�����n��һԪһ�η��̣��ⷽ�̼������n��ֵ����������м��ɵó����ۣ�
��������
��һ����n���ε�ÿ���ڽ�Ϊ144�㣬
��144n=180����n��2������ã�n=10��
�����n���ε����жԽ��ߵ������ǣ�==35��
��ѡC�� ��ͼ�����ı���ABCD�У�AB��DC��E��AD�е㣬EF��BC�ڵ�F��BC=5��EF=3��
��1����AB=DC�����ı���ABCD�����S=__��
��2����AB��DC�����ʱ�ı���ABCD�����S��__S���á�������=��������գ���

 (1)15����2��=��
�������������������1����AB=DC��AB��DC��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�����S=5��3=15��
��2����ͼ������EC���ӳ�CD��BE���ڵ�P��
��E��AD�е㣬
��AE=DE��
�֡�AB��CD��
���ABE=��P����A=��PDE��
�ڡ�ABE�͡�DPE�У�
�ߣ�
���ABE�ա�D...
(1)15����2��=��
�������������������1����AB=DC��AB��DC��
���ı���ABCD��ƽ���ı��Σ�
���ı���ABCD�����S=5��3=15��
��2����ͼ������EC���ӳ�CD��BE���ڵ�P��
��E��AD�е㣬
��AE=DE��
�֡�AB��CD��
���ABE=��P����A=��PDE��
�ڡ�ABE�͡�DPE�У�
�ߣ�
���ABE�ա�D... ��ͼ�������߾���A����1��0����B��5��0����C��0�� 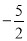 �����㣮
�����㣮
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�������һ��P��ʹPA+PC��ֵ��С�����P�����ꣻ
��3����MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��A��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�
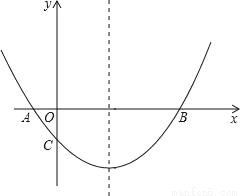
 ��1��y=x2��2x������2��P��2����������3����N��������4����������2+�� ����2���� ����
��������������������⿼����Ƕ��κ����ۺ��⣬�漰���ô���ϵ������һ�κ�������κ����Ľ���ʽ��ƽ���ıߵ��ж������ʡ�ȫ�������ε�֪ʶ���ڽ��3��ʱҪע����з������ۣ���1���������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ٰ�A����1��0����B��5��0����C��0��������������a��b��c...
��1��y=x2��2x������2��P��2����������3����N��������4����������2+�� ����2���� ����
��������������������⿼����Ƕ��κ����ۺ��⣬�漰���ô���ϵ������һ�κ�������κ����Ľ���ʽ��ƽ���ıߵ��ж������ʡ�ȫ�������ε�֪ʶ���ڽ��3��ʱҪע����з������ۣ���1���������ߵĽ���ʽΪy=ax2+bx+c��a��0�����ٰ�A����1��0����B��5��0����C��0��������������a��b��c... ��������y=x2��4x+4��y������ƽ��9����λ����������������x�������ύ�ڵ�B����y�ύ�ڵ�C������ΪD����1����B��C��D���ꣻ��2����BCD�������
 ��1����5��0������2��15.
�����������������
��1������ͼ��ƽ�ƵĹ�����������ߵĽ���ʽ���䷽��ɵö���D�����꣬��y=0���ɵ�B�����꣬��x=0���ɵ�C�����ꣻ
��2����D��DA��y���ڵ�A������ͼ�ε�����ĺ�������BCD�����.
���������
��1��������y=x2��4x+4��y������ƽ��9����λ�����ʽ��y=x2��4x+4��9����y=x2��4x��5��
...
��1����5��0������2��15.
�����������������
��1������ͼ��ƽ�ƵĹ�����������ߵĽ���ʽ���䷽��ɵö���D�����꣬��y=0���ɵ�B�����꣬��x=0���ɵ�C�����ꣻ
��2����D��DA��y���ڵ�A������ͼ�ε�����ĺ�������BCD�����.
���������
��1��������y=x2��4x+4��y������ƽ��9����λ�����ʽ��y=x2��4x+4��9����y=x2��4x��5��
... �ڶ��κ���y=ax2+bx+c�У����a��0��b��0��c��0����ô����ͼ��һ����������������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
 C
����������������
�١�a��0��c��0����������߿��ڷ������ϣ�����y�ύ�������
�ڡ�a��0��b��0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ�����x=����0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ����ڵ�һ���ޣ�
�ۺϢ٢ڣ����κ���y=ax2+bx+c��ͼ��һ���������������ޣ�
��ѡC��
C
����������������
�١�a��0��c��0����������߿��ڷ������ϣ�����y�ύ�������
�ڡ�a��0��b��0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ�����x=����0������κ���y=ax2+bx+c�ĺ���ͼ��ĶԳ����ڵ�һ���ޣ�
�ۺϢ٢ڣ����κ���y=ax2+bx+c��ͼ��һ���������������ޣ�
��ѡC�� ���꣬6��12��Ϊ����ڣ��ڶ����ǰϦ����λͬѧ��ij���е���һ�ֽ���Ϊ2Ԫ�����ӵ���������������С���ṩ����Ϣ�����С����С����������⣮
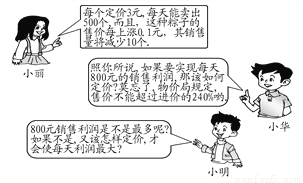
 (1)������Ϊ4Ԫʱ����ʵ��ÿ��800Ԫ����������(2)������Ϊ4.8Ԫʱ��ÿ��������������
�������������������1��С��������Ҫ��һԪ���η�������������Ĺؼ���Ū�壺��ʵ��ÿ��800Ԫ����Ķ���ΪxԪ/��ʱ��ÿһ�����ӵ�����Ϊ��x-2��Ԫ��һ��������500-��10�������ӣ����������з��̵ã���x-2)��500-��10��=800�����x1=4,x2=6����Ӧ����ʵ������ȷ������ֵ�Ƿ�...
(1)������Ϊ4Ԫʱ����ʵ��ÿ��800Ԫ����������(2)������Ϊ4.8Ԫʱ��ÿ��������������
�������������������1��С��������Ҫ��һԪ���η�������������Ĺؼ���Ū�壺��ʵ��ÿ��800Ԫ����Ķ���ΪxԪ/��ʱ��ÿһ�����ӵ�����Ϊ��x-2��Ԫ��һ��������500-��10�������ӣ����������з��̵ã���x-2)��500-��10��=800�����x1=4,x2=6����Ӧ����ʵ������ȷ������ֵ�Ƿ�... ��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ�����������涨����ѡ3�ˣ���ѡ��С�������¼�Ӧ����____��ѡ���Ȼ�¼����������¼�������¼�������
 ����¼�
�������������¼������Ŀ����Դ�С�ж���Ӧ�¼������ͼ��ɣ�
��𣺡�������
������¼���ָ��һ�������£����ܷ���Ҳ���ܲ��������¼�����
��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ��������
���涨����ѡ3�ˣ���Ů��Ҳѡ3�ˣ���ѡ��С�����Ŀ����Դ���һ��������
�ʴ�Ϊ������¼���
����¼�
�������������¼������Ŀ����Դ�С�ж���Ӧ�¼������ͼ��ɣ�
��𣺡�������
������¼���ָ��һ�������£����ܷ���Ҳ���ܲ��������¼�����
��10��ѧ����6��4Ů������С��ΪŮ�����У���ѡ6�˲μӡ�����֪ʶ��������
���涨����ѡ3�ˣ���Ů��Ҳѡ3�ˣ���ѡ��С�����Ŀ����Դ���һ��������
�ʴ�Ϊ������¼��� �߶�AB�غ�����ֱ�ķ���ƽ�Ƶ�A��B�䣬���߶�AB���߶�A��B���λ�ù�ϵ��__��
 ƽ�������
����������������
���߶�AB�غ�����ֱ�ķ���ƽ�Ƶ�A��B�䣬���߶�AB���߶�A��B���λ�ù�ϵ��ƽ������ȣ��ʴ�Ϊ��ƽ������ȣ�
ƽ�������
����������������
���߶�AB�غ�����ֱ�ķ���ƽ�Ƶ�A��B�䣬���߶�AB���߶�A��B���λ�ù�ϵ��ƽ������ȣ��ʴ�Ϊ��ƽ������ȣ� 
