题目内容
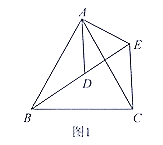
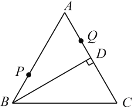
【题目】如图，等边△
中，
于
，
，点
、
分别为
、
上的两个定点且
，在
上有一动点
使
最短，则的最小值为_____
.
【答案】5
【解析】
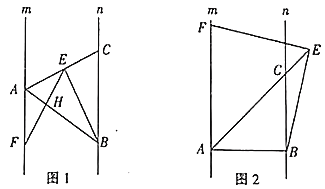
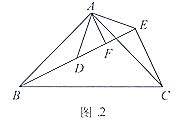
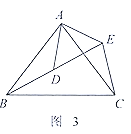
作点Q关于BD的对称点Q′，连接PQ′交BD于E，连接QE，此时PE+EQ的值最小，最小值PE+PQ=PE+EQ′=PQ′；
解：如图，∵△ABC是等边三角形，
∴BA=BC，
∵BD⊥AC，
∴AD=DC=3.5cm，
作点Q关于BD的对称点Q′，连接PQ′交BD于E，连接QE，此时PE+EQ的值最小．最小值PE+PQ=PE+EQ′=PQ′，
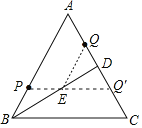
∵AQ=2cm，AD=DC=3.5cm，
∴QD=DQ′=1.5cm，
∴CQ′=BP=2cm，
∴AP=AQ′=5cm，
∵∠A=60°，
∴△APQ′是等边三角形，
∴PQ′=PA=5cm，
∴PE+QE的最小值为：5cm．
故答案为：5．
练习册系列答案
相关题目
【题目】某直销公司现有
名推销员，
月份每个人完成销售额（单位：万元），数据如下：
整理上面的数据得到如下统计表：
销售额 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
（1）统计表中的
；
；
（2）销售额的平均数是 ；众数是 ；中位数是 .
（3）
月起，公司为了提高推销员的积极性，将采取绩效工资制度：规定一个基本销售额，在基本销售额内，按
抽成；从公司低成本与员工愿意接受两个层面考虑，你认为基本销售额定位多少万元？请说明理由.
