题目内容
如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
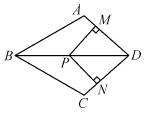
证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD.
又∵BA=BC,BD=BD,∴△ABD≌△CBD,
∴∠ADB=∠CDB.
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°.
又∵∠ADC=90°,∴四边形MPND是矩形.
∵∠ADB=∠CDB,PM⊥AD,PN⊥CD,
∴PM=PN,
∴四边形MPND是正方形.

练习册系列答案
相关题目
圆的对称性
| 圆的对称性 | 圆是轴对称图形,其对称轴是任意一条经过⑦ 的直线. | |
| 圆是中心对称图形,对称中心为⑧ . | ||
| 垂径定理 | 定理 | 垂直于弦的直径⑨ 弦,并且平分弦所对的两条⑩ . |
| 推论 | 平分弦(不是直径)的直径⑪ 弦,并且⑫ | |
| 圆心角、弧、弦之间的关系 | 在同圆或等圆中,如果两个圆心角﹑两条弧或两条弦中有一组量⑬ ,那么它们所对应的其余各组量也分别相等. |







 弦所对的两条弧.
弦所对的两条弧.