题目内容
2.在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合),如图1,DE与AC交于点P.
(1)求证:BD=DP;
(2)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;
(3)在图3中,DE与AC延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由.
分析 (1)过点D作DF⊥MN,交AB于点F,证得△BDF≌△PDA,可以证明BD=DP;
(2)过点D作DF⊥MN,交AB的延长线于点F,证得△BDF≌△PDA,可以证明BD=DP;
(2)过点D作DF⊥MN,交AB的延长线于点F,证得△BDF≌△PDA,可以证明BD=DP.
解答 (1)证明:如图1,过点D作DF⊥MN,交AB于点F,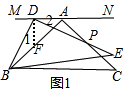
则△ADF为等腰直角三角形,
∴DA=DF.
∵∠1+∠FDP=90°,∠FDP+∠2=90°,
∴∠1=∠2.
在△BDF与△PDA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{DF=DA}\\{∠DFB=∠DAP=135°}\end{array}\right.$,
∴△BDF≌△PDA(ASA),
∴BD=DP.
(2)BD=DP成立.
证明:如图2,过点D作DF⊥MN,交AB的延长线于点F,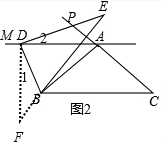
则△ADF为等腰直角三角形,
∴DA=DF.
∵∠1+∠ADB=90°,∠ADB+∠2=90°,
∴∠1=∠2.
在△BDF与△PDA中,
$\left\{\begin{array}{l}{∠1=∠2}\\{DF=DA}\\{∠DFB=∠DAP=45°}\end{array}\right.$,
∴△BDF≌△PDA(ASA),
∴BD=DP.
(3)BD=DP.
证明:如答图3,过点D作DF⊥MN,交AB的延长线于点F,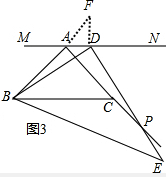
则△ADF为等腰直角三角形,
∴DA=DF.
在△BDF与△PDA中,
$\left\{\begin{array}{l}{∠F=∠PAD=45°}\\{DF=DA}\\{∠BDF=∠PDA}\end{array}\right.$,
∴△BDF≌△PDA(ASA),
∴BD=DP.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的性质等知识点,作辅助线构造全等三角形是解题的关键.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
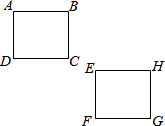 如图,正方形EFGH是由正方形ABCD平移得到的,则有( )
如图,正方形EFGH是由正方形ABCD平移得到的,则有( )| A. | 点E和B对应 | B. | 线段AD和EH对应 | C. | 线段AC和FH对应 | D. | ∠B和∠D对应 |
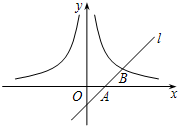 如图,已知直线l经过点A(1,0),与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1).过点P(p,p-1)(其中p>1)作 轴的平行线分别交双曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于点M、N.
如图,已知直线l经过点A(1,0),与双曲线y=$\frac{m}{x}$(x>0)交于点B(2,1).过点P(p,p-1)(其中p>1)作 轴的平行线分别交双曲线y=$\frac{m}{x}$(x>0)和y=-$\frac{m}{x}$(x<0)于点M、N.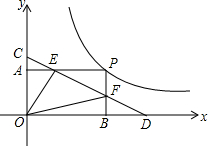 如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( )
如图.矩形OAPB的顶点P在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点E、F分别是矩形的边PA,PB上的动点,直线EF分别交y轴、x轴于C,D两点.现给出如下命题:①若点E、F恰同在反比例函数y=$\frac{m}{x}$(k>m>0)的图象上,则S四边形OEPF=k-m;②△ACE≌△BFD;③若OC=OD=$\sqrt{2k}$,则△OCF∽△EOF;④CE+DF=EF.其中结论正确的是( ) 如图,直线a∥b,则∠A=20°,若作BH⊥AC于H,则∠ABH=70°.
如图,直线a∥b,则∠A=20°,若作BH⊥AC于H,则∠ABH=70°. 如图,∠2+∠D=180°,∠1=∠B,那么AB∥EF吗?为什么?
如图,∠2+∠D=180°,∠1=∠B,那么AB∥EF吗?为什么? 已知:∠ACB=∠ABD=90°,AB=$\sqrt{6}$,AC=2,求AD的长为多少时,图中两直角三角形相似?
已知:∠ACB=∠ABD=90°,AB=$\sqrt{6}$,AC=2,求AD的长为多少时,图中两直角三角形相似?