题目内容
 有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|+|a-b|.
有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|+|a-b|.考点:整式的加减,数轴,绝对值
专题:
分析:由图知,b>0,a-c<0,b-c>0,a-b<0,根据正数的绝对值等于它本身,负数的绝对值等于它的相反数可得,|b|+|a-c|+|b-c|+|a-b|=b+c-a+b-c+b-a=3b.
解答:解:由数轴得,a<c<0<b,
∴b>0,a-c<0,b-c>0,a-b<0,
∴|b|+|a-c|+|b-c|+|a-b|=b+c-a+b-c+b-a=3b-2a.
∴b>0,a-c<0,b-c>0,a-b<0,
∴|b|+|a-c|+|b-c|+|a-b|=b+c-a+b-c+b-a=3b-2a.
点评:本题考查了整式的加减,绝对值与数轴,用两种不同的方法即几何方法和代数方法进行求解.通过比较,可以发现借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小有直观、简捷,举重若轻的优势.

练习册系列答案
相关题目
函数y=ax2(a≠0)的图象与a无关的是( )
| A、顶点坐标不同 |
| B、对称轴相同 |
| C、开口方向一致 |
| D、都有最大值 |
 如图,AO交⊙O于点C,过⊙O上一点P,作PF⊥OA,垂足为F,直线PF交⊙O于点E,∠FPC=∠CPA,请问PA是⊙A的切线吗?为什么?
如图,AO交⊙O于点C,过⊙O上一点P,作PF⊥OA,垂足为F,直线PF交⊙O于点E,∠FPC=∠CPA,请问PA是⊙A的切线吗?为什么?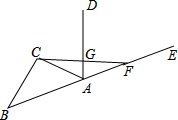 如图,已知△ABC,作△ABC的外角∠EAC的平分线AD,在射线AE上截取AF=AC,连接CF交AD于点G.试猜想AG与CF的位置关系,并证明你的猜想.
如图,已知△ABC,作△ABC的外角∠EAC的平分线AD,在射线AE上截取AF=AC,连接CF交AD于点G.试猜想AG与CF的位置关系,并证明你的猜想.