题目内容
18. 如图,△ABC中AD是∠A的平分线,E是AD的中点,EF⊥AD交BC的延长线于F.求证:DF2=CF•BF.
如图,△ABC中AD是∠A的平分线,E是AD的中点,EF⊥AD交BC的延长线于F.求证:DF2=CF•BF.
分析 利用垂直平分线的性质得出AF=DF,进而利用外角的性质得出∠B=∠1,即可得出△ACF∽△BAF,即可得出答案.
解答  证明:连接AF,
证明:连接AF,
∵AD的垂直平分线交BC的延长线于F,
∴AF=DF,
∴∠1+∠2=∠4,
∵∠B+∠3=∠4,∠2=∠3,
∴∠B=∠1,
∵∠AFB=∠CFA,
∴△ACF∽△BAF,
∴$\frac{AF}{BF}$=$\frac{CF}{AF}$,
∴AF2=CF•BF,
即DF2=CF•BF.
点评 此题主要考查了相似三角形的判定与性质,根据已知得出∠B=∠1是解题关键.

练习册系列答案
相关题目
6.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在二次函数y=-2x2的图象上,则y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y3>y1 | C. | y3>y2>y1 | D. | y2>y1>y3 |
10. 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )
 如图所示的正方体,如果把它展开,可以得到( )
如图所示的正方体,如果把它展开,可以得到( )| A. |  | B. |  | C. |  | D. |  |
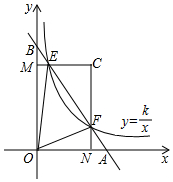 如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.
如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.