题目内容
9.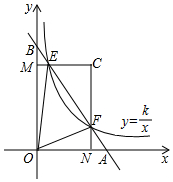 如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.
如图,平面坐标系中,AB交矩形ONCM于E、F,若$\frac{BE}{BF}$=$\frac{1}{m}$(m>1),且双曲线y=$\frac{k}{x}$也过E、F两点,记S△CEF=S1,S△OEF=S2,用含m的代数式表示$\frac{{s}_{1}}{{s}_{2}}$.
分析 过点F作FG⊥y轴于点G,根据平行线证出三角形相似得出ME:MC的值,设出点C的坐标,表示出点E、F的坐标,结合三角形的面积公式找出S1、S2的值,二者相比即可得出结论.
解答 解:过点F作FG⊥y轴于点G,如图所示:
∵CM⊥y轴,FG⊥y轴,
∴CM∥FG,MC=FG,
∴△BME∽△BGF,
∴$\frac{ME}{MC}$=$\frac{ME}{GF}$=$\frac{BE}{BF}$=$\frac{1}{m}$,
设点C的坐标为(a,b),则E($\frac{a}{m}$,b),F(a,$\frac{b}{m}$),
∴S1=$\frac{1}{2}$×(a-$\frac{a}{m}$)•(b-$\frac{b}{m}$)=$\frac{(m-1)^{2}}{2{m}^{2}}$ab;
S2=a•b-$\frac{1}{2}$•$\frac{ab}{m}$-$\frac{1}{2}$•$\frac{ab}{m}$-$\frac{(m-1)^{2}}{2{m}^{2}}$ab=$\frac{{m}^{2}-1}{2{m}^{2}}$ab.
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{m-1}{m+1}$.
点评 此题主要考查了相似三角形的判定与性质、反比例函数的综合应用以及三角形面积求法,根据已知表示出E,F的点坐标是解题关键.

练习册系列答案
相关题目
1.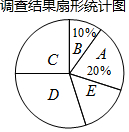 近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表
近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表
请根据图表中提供的信息解答下列问题:
(1)填空:m=80,n=100,扇形统计图中E组所占的百分比为15%
(2)若该市人口约有400万人,请你计算其中持D组“观点”的市民人数.
(3)对于“雾霾”这个环境问题,请用简短的语言发出倡议.
 近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表
近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表| 组别 | 观点 | 频数(人数) |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 40 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
(1)填空:m=80,n=100,扇形统计图中E组所占的百分比为15%
(2)若该市人口约有400万人,请你计算其中持D组“观点”的市民人数.
(3)对于“雾霾”这个环境问题,请用简短的语言发出倡议.
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-2),B(3,-1),C(1,-1).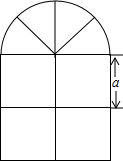 如图,一个窗户的上部为半圆形,下部是由边长均为acm的4个小正方形组成的正方形,计算这个窗户的面积和窗户外框的总长.
如图,一个窗户的上部为半圆形,下部是由边长均为acm的4个小正方形组成的正方形,计算这个窗户的面积和窗户外框的总长. 如图,△ABC中AD是∠A的平分线,E是AD的中点,EF⊥AD交BC的延长线于F.求证:DF2=CF•BF.
如图,△ABC中AD是∠A的平分线,E是AD的中点,EF⊥AD交BC的延长线于F.求证:DF2=CF•BF.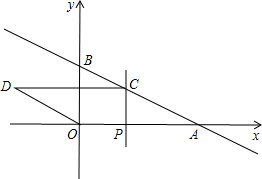 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造?OACD,设点P的横坐标为m.
如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造?OACD,设点P的横坐标为m.