Question

【题目】如图，为了绿化小区，某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH．

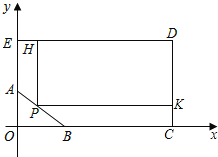
已知：，DE＝100米，EA＝60米，BC＝70米，CD＝80米．以BC所在直线为x轴，AE所在直线为y轴，建立平面直角坐标系，坐标原点为O．

（1）求直线AB的解析式．

（2）若设点P的横坐标为x，矩形PKDH的面积为S，求S关于x的函数关系式．

Answer 1

【答案】（1）；（2）

【解析】

（1）根据题意易求A、B的坐标为（0，20）、（30，0）．利用待定系数法可以求得直线AB的解析式；

（2）点P的坐标可以表示为（x，-x+20），则PK=100-x，PH=80-（-x+20）=60+x，所以根据矩形的面积公式可以求得函数解析式为：S=（100-x）（60+x）．

解：（1）如图所示，∵OE＝80米，OC＝ED＝100米，AE＝60米，BC＝70米，

∴OA＝20米，OB＝30米，

即A、B的坐标为（0，20）、（30，0）．

设直线AB的解析式为（k≠0），则，

解得，，

则直线AB的解析式为；

（2）设点P的坐标为P（x，y）．

∵点P在直线AB上，所以点P的坐标可以表示为，

∴，，

∴．