Question

【题目】阅读以下材料，并按要求完成相应的任务．如图（1），已知四边形ABCD的对角线AC，BD相交于点O，点M是BC边的中点，过点M作ME∥AC交BD于点E，作MF∥BD交AC于点F．我们称四边形0EMF为四边形ABCD的“伴随四边形”．

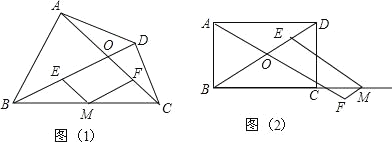
（1）若四边形ABCD是菱形，则其“伴随四边形”是　 　，若四边形ABCD矩形，则其“伴随四边形”是：　 　（在横线上填特殊平行四边形的名称）

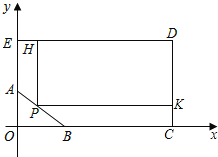
（2）如图（2），若四边形ABCD是矩形，M是BC延长线上的一个动点，其他条件不变，点F落在AC的延长线上，请写出线段OB、ME，MF之间的数量关系，并说明理由．

Answer 1

【答案】（1）矩形；菱形

（2）证明见解析.

【解析】

（1）根据矩形、菱形的性质定理和判定定理进行证明即可；

（2）根据平行四边形的性质得到OE=MF，得到OB+MF=BE，根据平行线的性质和等腰三角形的性质得到EB=EM，证明结论．

（1）如图1，∵ME∥AC，MF∥BD，

∴四边形OEMF是平行四边形，

∵四边形ABCD是菱形，

∴AC⊥BD，

∴∠BOC＝90°，

∴四边形OEMF是矩形；

如图2，∵ME∥AC，MF∥BD，

∴四边形OEMF是平行四边形，

∵四边形ABCD是矩形，

∴OB＝OC，

∵M是BC边的中点，

∴ME＝OC，MF＝OB，

∴ME＝MF，

∴四边形OEMF是菱形；

故答案为：矩形；菱形．

（2）∵ME∥AC，MF∥BD，

∴四边形OEMF是平行四边形，

∴OE＝MF，

∴OB+MF＝OB+OE＝BE，

∵四边形ABCD是矩形，

∴∠OBC＝∠OCB，

∵ME∥AC，

∴∠EMB＝∠OCB，

∴∠EBM＝∠EMB，

∴EB＝EM，

∴EM＝OB+MF．